指数関数とは、a > 0 かつ a ≠ 1 のとき「 y = ax で表される関数」のことを言います。
また、この関数 y = ax のことを「 a を底とする x の指数関数」と呼びます。
a > 1 のとき、指数関数は x が増加するにつれて y の値が増加していき
1 > a > 0 のとき、指数関数は x が増加するにつれて y の値が減少していくという特徴があります。

このページでは、「指数と関数の意味」から指数関数とは何なのかを見ていきましょう。
指数とは
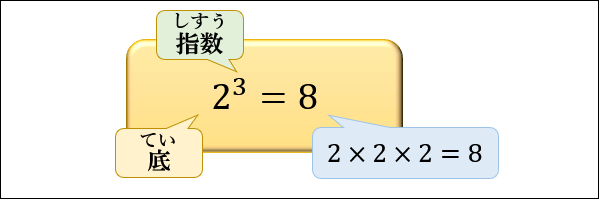
\(2\) を \(3\) 回かけ算すると、\(2×2×2=8\) になりますよね。
これを「 \(2\) を \(3\) 乗したら \(8\) になる」と言い、次のように書きます。
このとき
繰り返しかけ算する数「 \(2\) 」のことを「底」
「底」を繰り返しかけ算する回数「 \(3\) 」のことを「指数」
と言います。
「指数」とは、「底」を繰り返しかけ算する回数を表す値
関数とは
「変数 \(x\) によって値が決まる数」のことを、「関数」と言います。
たとえば、時給 \(800\) 円の仕事があった場合
働く時間を \(x\) 時間、もらえる給料を \(y\) 円とおくと
\(y=800x\) と表せて、「働く時間 \(x\) によって給料 \(y\) の値が決まる」ことが分かりますよね。
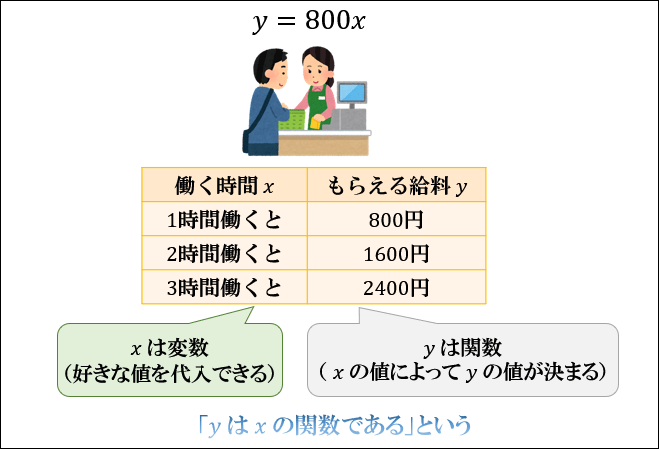
このとき、「給料 \(y\) は働く時間 \(x\) の関数である」と言います。
「関数」とは、変数 \(x\) によって値が決まる数のこと
指数関数とは
指数関数とは、「指数」の部分が変数 \(x\) である「関数」のことです。

具体的には
「定数 \(a\) を繰り返しかけ算する回数」が変数 \(x\) となった関数 \(y=a^x\) のことを
「 \(a\) を底とする \(x\) の指数関数」と言います。
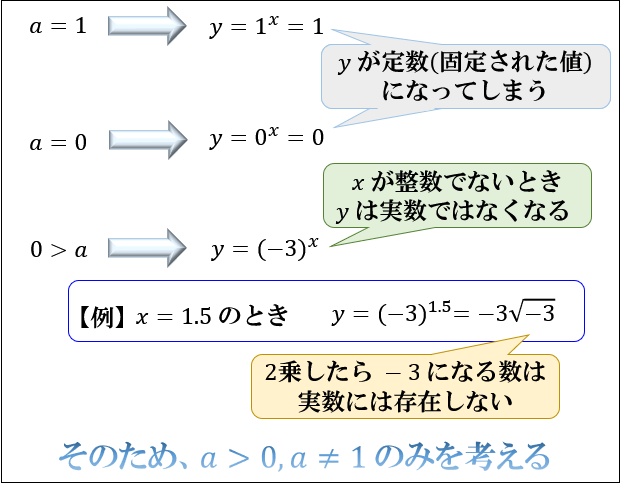
指数関数 \(y=a^x\) では、\(「a>0,a≠1」\)の場合のみを考えるのが一般的です。
\(a=1\) や \(0≧a\) だと、 \(y=a^x\) が定数になったり、実数ではなくなるケースがあるからです。
4つの指数法則
指数関数を使いこなすには、\(4\) つの指数法則を知っておくことが重要です。
【指数法則】
\(a\neq0\) かつ \(m,n\) が整数のとき
- \(a^m×a^n=a^{(m+n)}\)
- \((a^m)^n=a^{mn}\)
- \(a^{-n}=\frac{1}{a^n}\)
- \(a^{\frac{1}{n}}=\sqrt[n]{a}\)
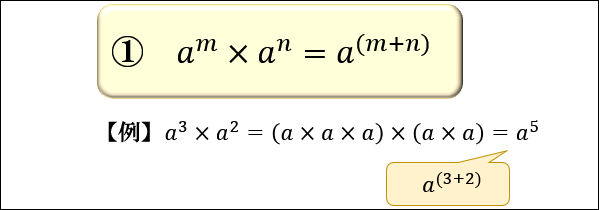
1つ目は、「\(a\) を \(m\) 回かけた値」に「\(a\) を \(n\) 回かけた値」をかけると
「\(a\) を \((m+n)\) 回かけた値」になる、というものです。
この法則に \(n=0\) を代入して \(a^m\) で割ると、\(a^0=1\) であることも分かります。

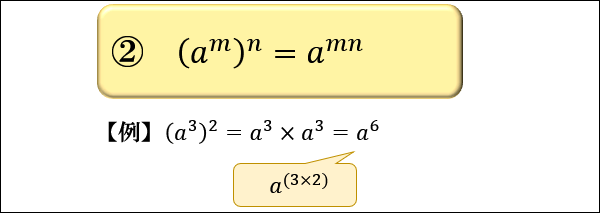
2つ目は、「\(a\) を \(m\) 回かけた値」を \(n\) 回かけると
「\(a\) を \(m×n\) 回かけた値」になる、というものです。
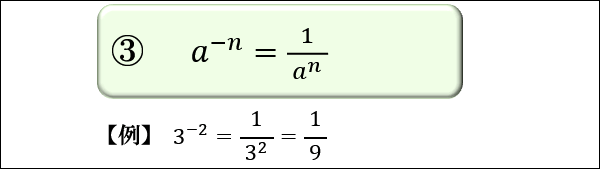
3つ目は、「\(a\) の \(-n\) 乗」は「\(a\) の \(n\) 乗の逆数」になるというもの。
この法則は、1番目の法則に \(m=-n\) を代入して両辺を \(a^n\) で割ると求まります。
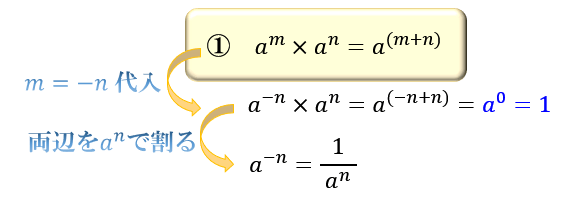
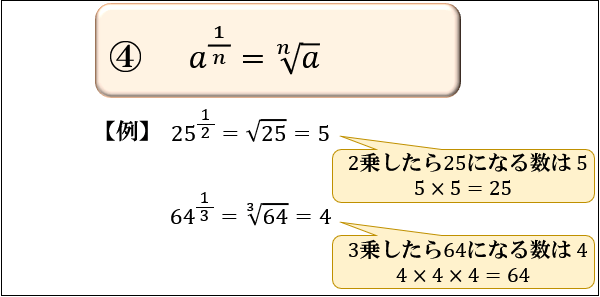
4つ目は、「\(a\) の \(\frac{1}{n}\) 乗」は「\(a\) の \(n\) 乗根」になるというもの。
※ \(a\) の \(n\) 乗根:「\(n\) 乗したら \(a\) になる数」のこと
この法則は、2番目の法則に \(m=\frac{1}{n}\) を代入すると求まります。

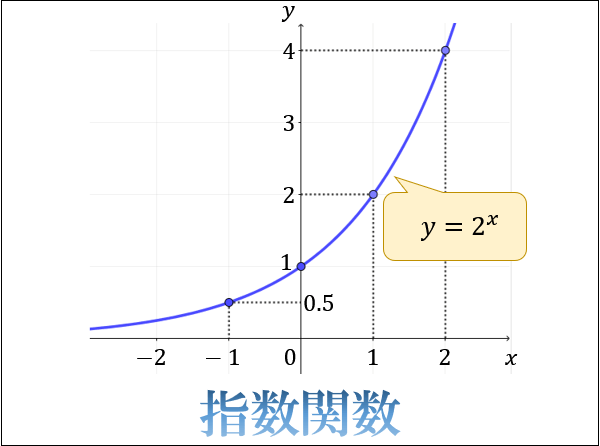
指数関数をグラフで見てみよう
指数関数のグラフは、\(y=a^x\) を満たす \((x,y)\) の点を滑らかにつないでいくと描くことができます。
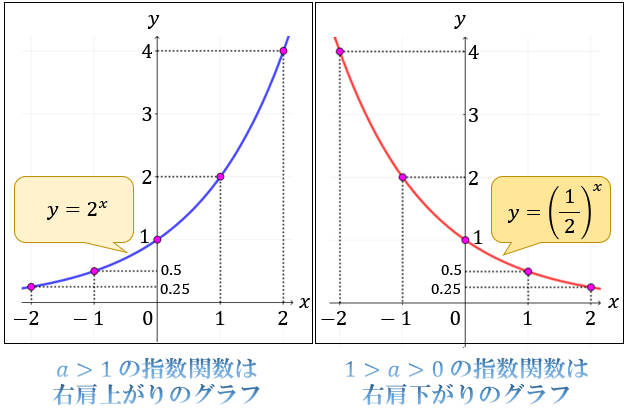
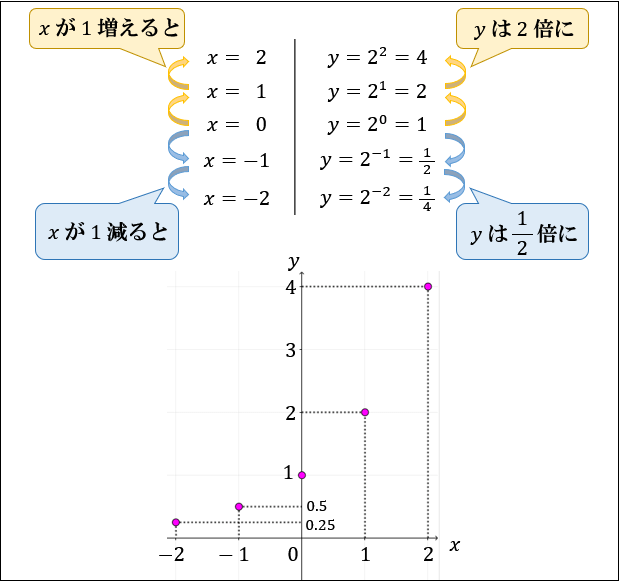
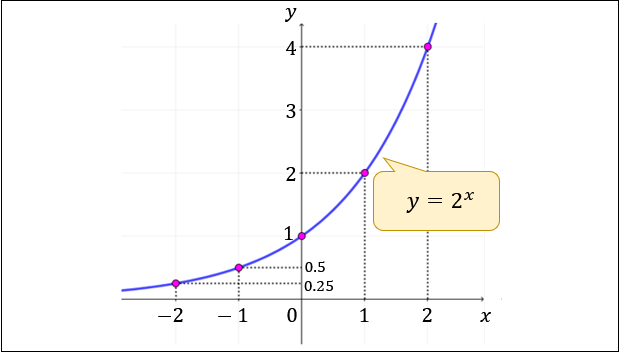
たとえば「\(y=2^x\)」を作図するときは「\(x=0\) のとき \(y=2^0=1\)」をベースに
\(x\) が \(1\) 増えるごとに \(y\) は \(2\) 倍される
\(x\) が \(1\) 減るごとに \(y\) は \(\dfrac{1}{2}\) 倍される
と考えると作図しやすいです。
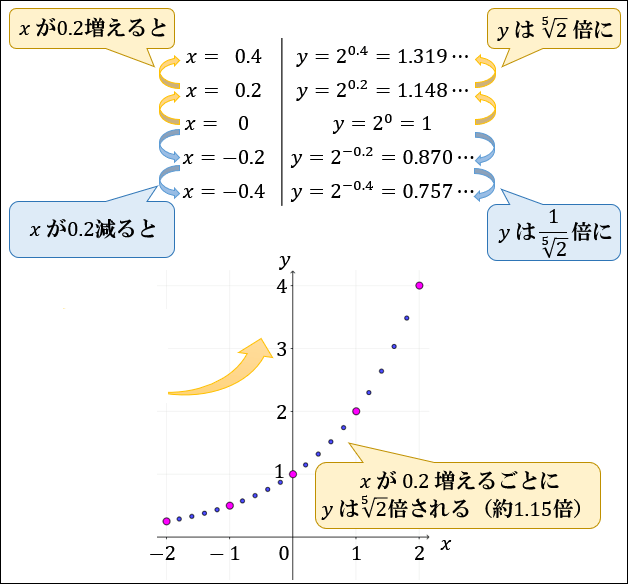
ここからさらに細かく見ていくには、「\(2\) の \(n\) 乗根」を使います。
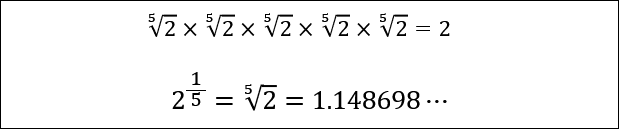
たとえば \(2\) の \(5\) 乗根 \(\sqrt[5]{2}≒1.148\) を使うと
\(x\) が \(0.2\) 増えるごとに \(y\) は \(\sqrt[5]{2}≒1.148\) 倍される
\(x\) が \(0.2\) 減るごとに \(y\) は \(\dfrac{1}{\sqrt[5]{2}}≒0.870\) 倍される
ということが分かります。
これを図に反映すると以下のようになります。
これを繰り返していくと、最終的に \(y=2^x\) は以下のグラフになることが分かります。
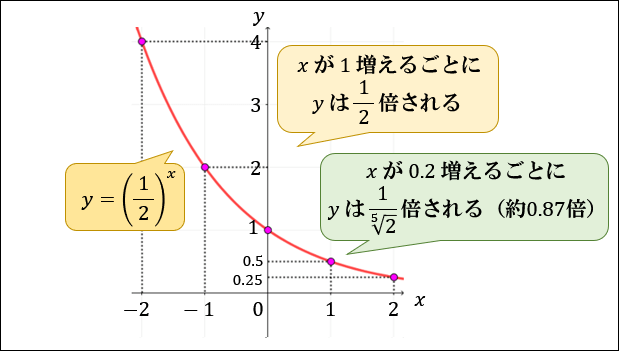
\(y=\left(\dfrac{1}{2}\right)^x\) の場合は、同様の手順をふむと以下のグラフになることが分かります。
指数関数の性質
最後に、指数関数 \(y=a^x\) の性質です。
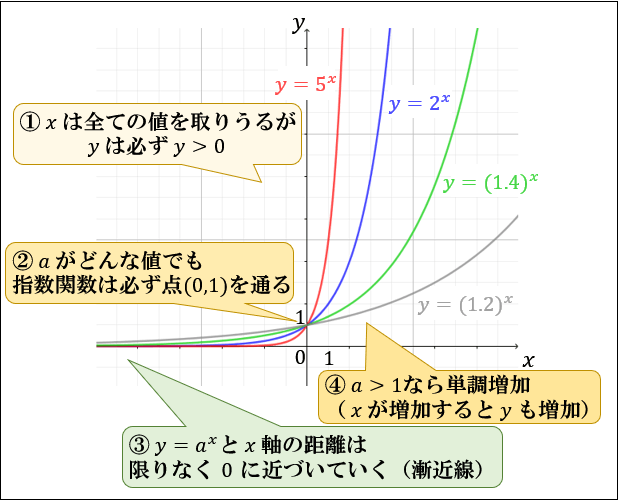
- \(-∞<x<∞,y>0\)
- \(a\) がどんな値でも必ず点 \((0,1)\) を通る
- 漸近線は \(x\) 軸 \((y=0)\)
- \(a>1\) なら単調増加(\(x\) が増加すると \(y\) も増加)
- \(1>a>0\) なら単調減少(\(x\) が増加すると \(y\) は減少)