数には色々な集合があります。
自然数・整数・有理数・無理数・実数。
実数全体の話をしているときに整数だけの話だと勘違いしてしまったり、自然数に限定した話をしているときに有理数全体の話だと勘違いしてしまうのは珍しいことではありません。
うっかり間違えてしまうと思いがけないミスにつながってしまいます。
ここで、改めて確認してみて下さい。
photo credit:Artiom Gorgan
物を数える「自然数」
自然数とは、物を数えるのに使う「1,2,3,…」と続いていく数の総称です。
「自然数とは、正の整数 1,2,3,… のことである」
「0や負の整数 -1,-2,…は、自然数に含まれない」
ややこしいですが、「0」は自然数には含まれません。
「ここに、0個のりんごがあります」
「彼女の順位は1位で、彼の順位は0位です」
といった表現は「自然」ではないですよね。
大学以降の集合論などにおいては「0も自然数に含まれる」という流儀もありますが、少なくとも中学・高校数学においては「0は自然数に含まれない」でOKです。
マイナスも含む「整数」
整数とは、「0」と、0に1ずつ加えていって得られる「1,2,3,…」と、0から1ずつ引いていって得られる「-1,-2,-3,…」の総称です。
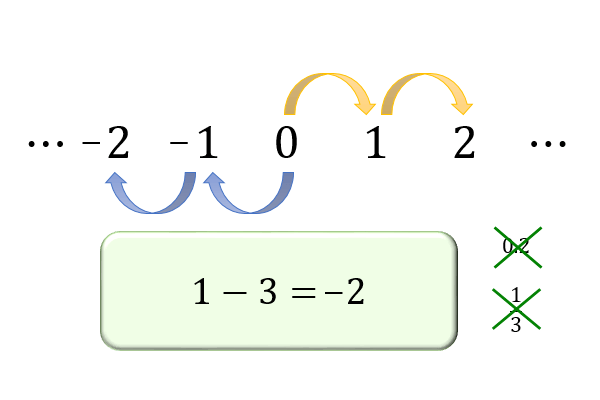
「昨日の気温は1℃だったが、今日はそれよりも3℃低い『マイナス2℃』だった」
といったように、整数では「0よりも小さな数」を考えられるようになります。
整数の比で表せる「有理数」
整数だけだと、「1リットルの水を3人で分けたら1人当たり何リットルもらえる?」といったように割り算をしたいときに困ったことになります。
そこで登場するのが有理数です。
有理数とは、「整数の比で表される数」のこと。
より正確に言うと「2つの整数 a , b を使って a/b と表せる数」を指します。

①整数は、有理数に含まれます。5=5/1のように整数はすべて「整数の比」で表せるからです。
②有限小数も、有理数に含まれます。0.173=173/1000のように有限小数もすべて「整数の比」で表せるからです。
③循環小数も、有理数に含まれます。0.333…=1/3といったように循環小数もすべて「整数の比」で表せることが分かっているからです。
※有限小数:0.173のように小数点以下の桁数が有限の小数
※循環小数:1/7=0.142857142857142…のように同じ数字の列が無限に繰り返される小数
実在するすべての数である「実数」
有理数とは反対に、整数の比で表せない数のことを無理数と言います。
無理数は、循環することなく無限に続く小数です。
例えば
円周率 π=3.14159265…
ネイピア数 e=2.71828182…
2の平方根 √2=1.41421356…
自然対数 loge10=2.30258509…
などが無理数であることが分かっています。
(πとeについては下記記事を参考に)


そして、有理数と無理数を合わせた全体を「実数」と言います。
下図のイメージでおさえておくと、それぞれの数の関係が分かりやすいです。
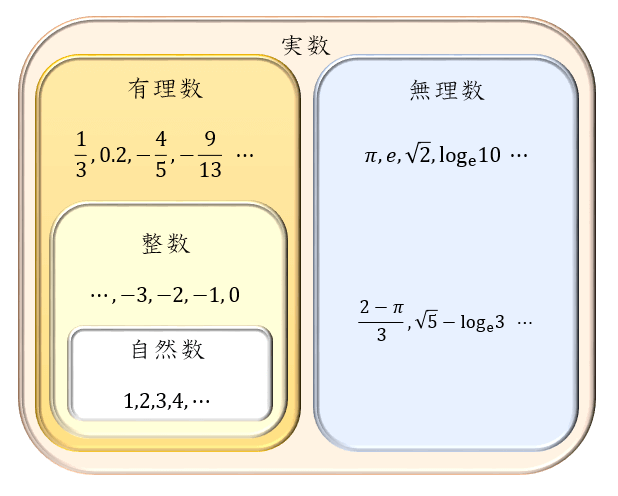
それまで使っていた数では表せない数が出てくるたびに、数の領域はどんどん拡張されていきます。いきなりすべてを理解する必要はないので、1つずつ積み重ねていきましょう!