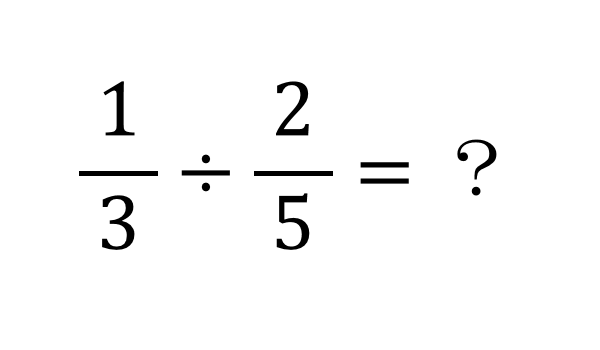2つのベクトルに対して、以下の式で表される値をベクトルの内積と言います。

内積は「ドット積」(英語で dot product)とも呼ばれる
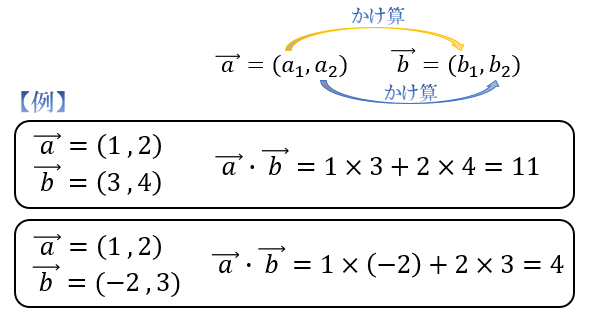
たとえば、\((1,2)\) と \((3,4)\) の内積は、\(1×3+2×4=11\) となります。
内積は「こういう値を定義しておくと色んな使い道があって便利」くらいの意味合いの数値です。
今回は、そんな内積の考え方と使い道を見ていきましょう。
内積の定義
ベクトルの内積には、2つの定義の仕方があります。
1つは幾何学(図形・空間の性質について研究する分野)による定義。
もう1つは代数学(文字を用いて方程式の解法を研究する分野)による定義です。
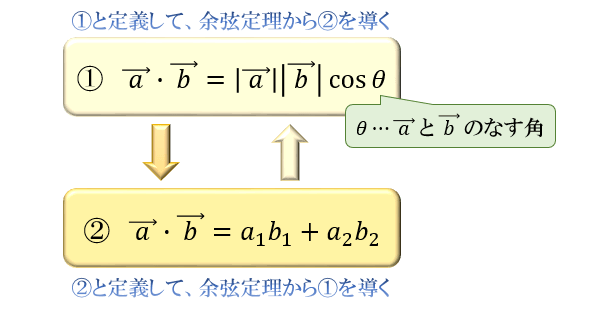
① \(\vec{\ a\ }\cdot\vec{\ b\ }=|\vec{\ a\ }||\vec{\ b\ }|\cos{θ}\) と定義する(幾何的定義)
② \(\vec{\ a\ }\cdot\vec{\ b\ }=a_1b_1+a_2b_2\) と定義する(代数的定義)
片方の式で内積を定義すれば、余弦定理からもう片方の式を導きだせるので、どちらで定義しても問題ありません。
ただ、
● いきなり①と定義すると「なぜ急に \(\cos{θ}\) が出てくるのか」に戸惑いやすい
● \(n\) 次元ベクトルの内積の定義は②の形のほうが一般的
● 「②の式から内積を求め、②=①を使って \(\cos{θ}\) を求める」のような使い方をする
といった理由から「②と定義し、余弦定理から①が導かれる」と考えた方が理解しやすいです。
内積の求め方
内積を理解するために、例題を解いてみましょう。
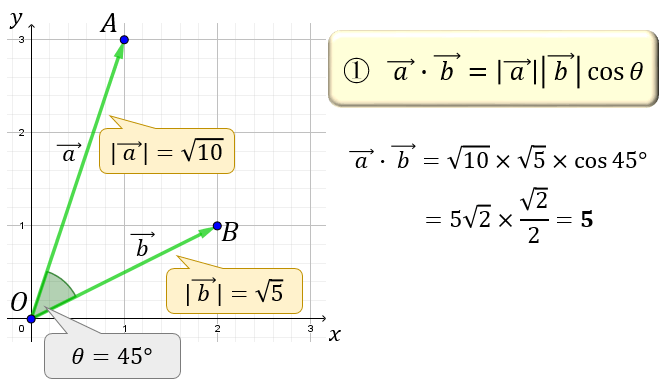
【例題】\(\vec{\ a\ }=(1,3),\) \(\vec{\ b\ }=(2,1),\) \(|\vec{\ a\ }|=\sqrt{10},\) \(|\vec{\ b\ }|=\sqrt{5},\) \(\vec{\ a\ }\) と \(\vec{\ b\ }\) のなす角 \(θ=45°\) とする。このとき、2つのベクトルの内積は?
まずは、①の式を用いた求め方。
次は、②の式を用いた求め方。
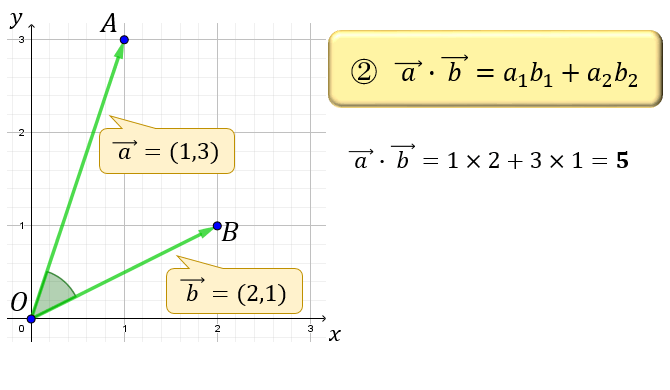
どちらの式を使っても、2つのベクトルの内積が \(5\) になることが分かります。
内積の具体的な活用法
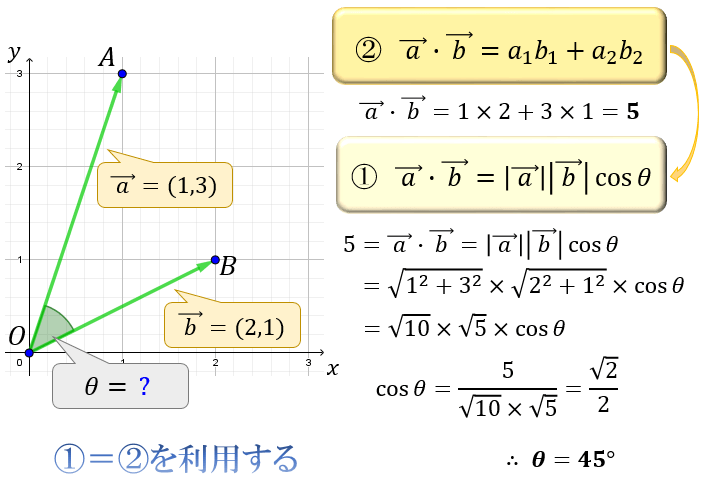
内積の活用法は色々ありますが、その中の1つに「①=②が成り立つことを利用して2つのベクトルの角度を手軽に把握・計算する」という使い方が挙げられます。
例えば、先ほどの例題では2つのベクトルのなす角は \(θ=45°\) と与えられていましたが、もし \(θ\) の値が分かっておらず、\(θ\) の値を知りたいという状態の場合。
内積の①=②という性質を利用すれば素早く角度を求めることができます。
カンタンに \(\cos{θ}\) が求まるということは「カンタンに \(\vec{\ b\ }\cos{θ}\) が求まる」 ということでもあります。
そのため「操作キャラクターが物体に斜めに衝突したときの力のかかり方や移動距離」を計算したいときも、内積をプログラミング上で定義しておくと便利です。

内積のこの性質は3次元ベクトルに拡張しても成り立つので、3次元空間上の計算にも応用がききます。