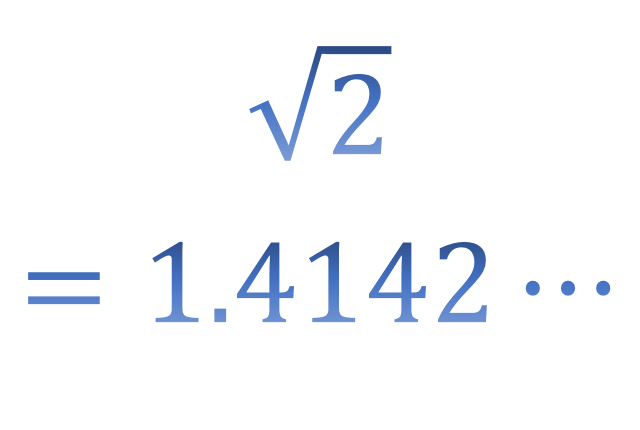
財布の中に \(200\) 円ある。いま、その財布の中に \(300\) 円を入れた。
このとき、財布の中には何円入っていますか?

答えは、\(200+300=500\) 円ですね。
このように、多くの算数・数学の問題では「大きさ」だけの量を使って計算をします。
それでは、次のような問題の場合はどうでしょうか。
自宅から東に \(1\) km 進んだあと、北に \(1\) km 進んだところにコンビニがある。
このコンビニは自宅から見て、どの方向にどのくらい離れた場所にある?
この問題の場合、答えは \(1+1=2\) km とはなりません。
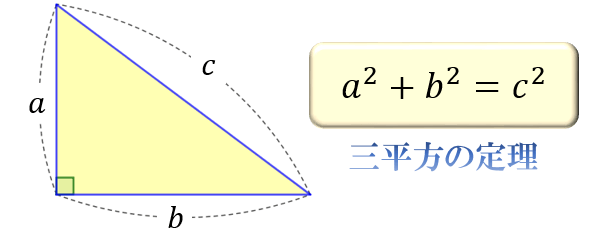
三平方の定理を使って、 \(\sqrt{1^2+1^2}=\sqrt{2}≒1.41\) より
「自宅から見て、北東に約 \(1.41\) km離れた場所にある」が答えとなります。
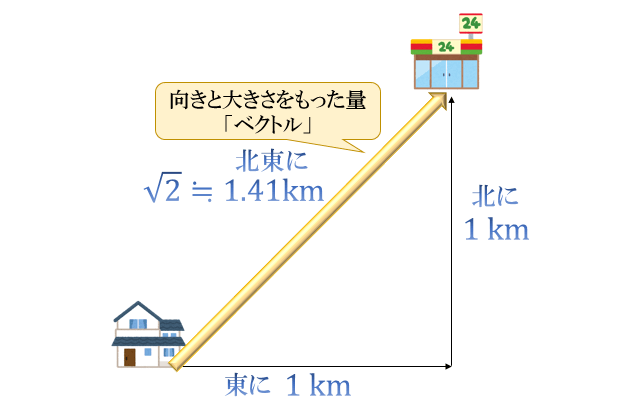
このように、「大きさ」に加えて「向き」も持った量を使うことで
2次元平面や3次元空間上のものごとを数式に取り入れて考えることが可能になります。
この「大きさ」だけでなく「向き」も持った量。
それが、ベクトルです。
このページでは、ベクトルの基礎を解説していきます。
ベクトルとは?
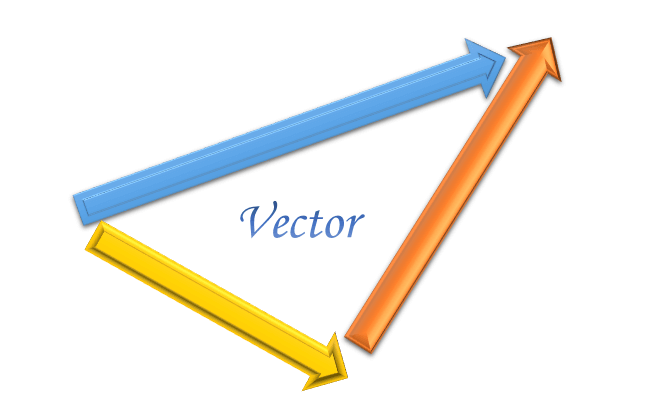
ベクトルとは、向きと大きさをもった量のこと。英語では Vector と書きます。
ベクトルは、矢印がベクトルの「向き」を表し、長さがベクトルの「大きさ」を表しています。
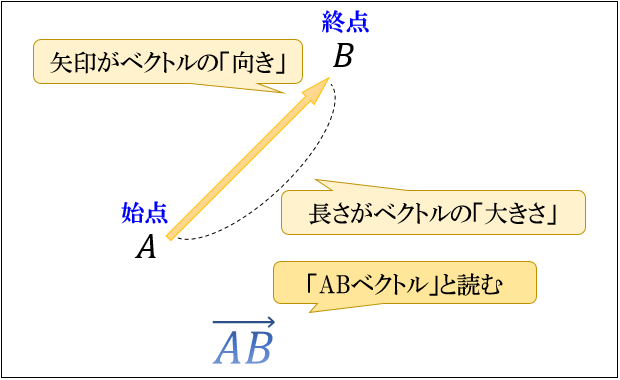
ここで
矢印の始まりである点を「始点」
矢印の終わりである点を「終点」
点Aを始点、点Bを終点とするベクトルを \(\vec{AB}\) と書いて「ABベクトル(ベクトルAB)」
と言います。
反対に、点Bから点Aに向けたベクトルは \(\vec{BA}\) と書きます。
※ \(\vec{BA}=-\vec{AB}\)
向きと大きさが同じなら、位置は関係がない
ベクトルは、向きと大きさが同じであれば「位置は問題にしない」という特徴があります。
「向き」と「大きさ」が等しいものは、すべて同一のベクトルとみなされます。
たとえば、下図の \(\vec{CD}\) は \(\vec{AB}\) を左上に平行移動させたものです。
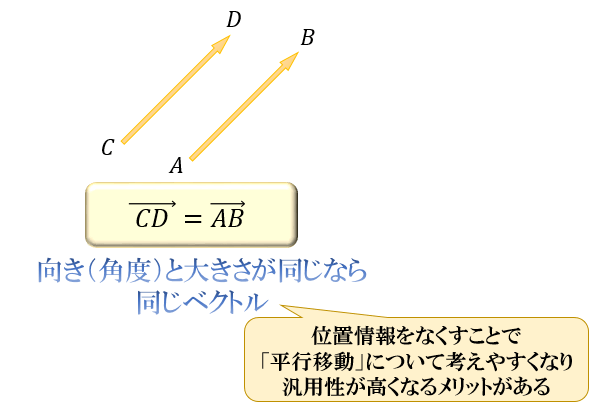
このとき、\(\vec{CD}\) と \(\vec{AB}\) は「向き」と「大きさ」が同じなので、互いに等しいベクトル、つまり \(\vec{CD}=\vec{AB}\) ということになります。
ベクトルの表現方法
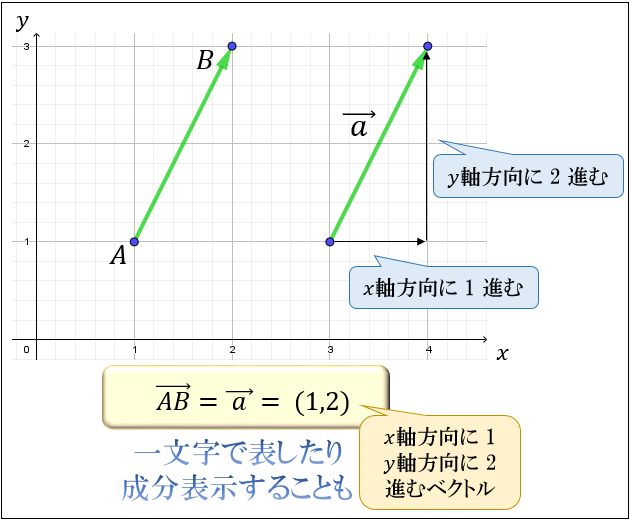
ベクトルは始点・終点を記号で明示せずに、単に \(\vec{\ a\ }\) と表現することもできます。
他にも、\(x\) 軸方向に \(1\) 、\(y\) 軸方向に \(2\) 進むベクトルなら \((1,2)\) というように ( \(x\) 軸 \(,y \) 軸) の形で成分表示することも可能です。
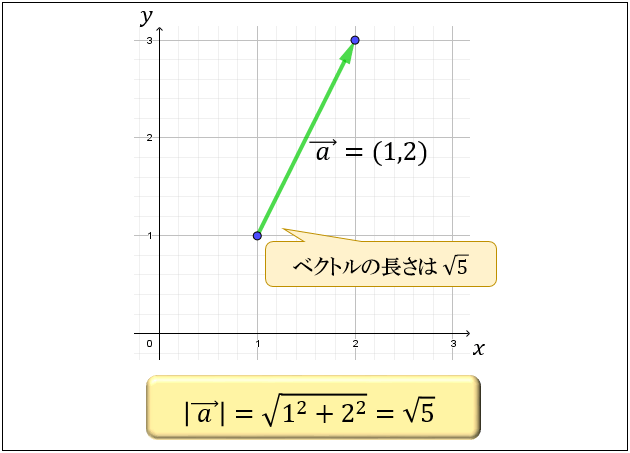
ベクトルの長さ
ベクトル \(\vec{\ a\ }=(a_1,a_2)\) に対して
このベクトルの長さは \(|\vec{\ a\ }|=\sqrt{{a_1}^2+{a_2}^2}\) で表されます。
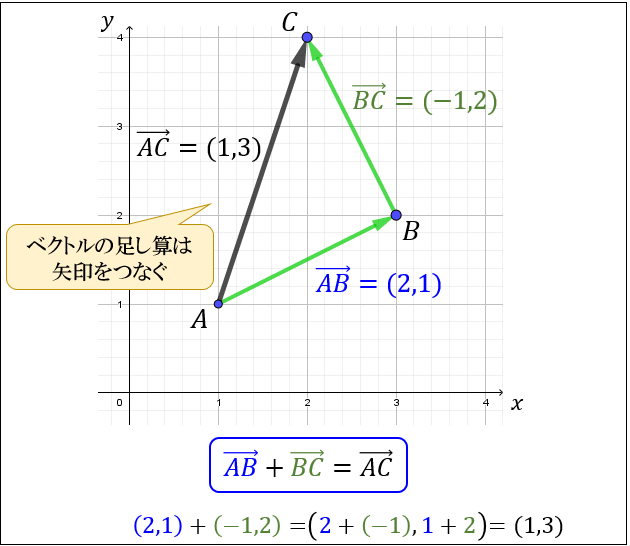
ベクトルの足し算
2つのベクトル \(\vec{\ a\ }=(a_1,a_2)\) と \(\vec{\ b\ }=(b_1,b_2)\) に対して
この2つのベクトルの足し算は
\(\vec{\ a\ }+\vec{\ b\ }=(a_1+b_1,a_2+b_2)\) で表されます。
3つの点 \(A,B,C\) を用いて \(\vec{AB}+\vec{BC}=\vec{AC}\) が成り立つという性質もあります。
ベクトルの引き算
2つのベクトル \(\vec{\ a\ }=(a_1,a_2)\) と \(\vec{\ b\ }=(b_1,b_2)\) に対して
この2つのベクトルの引き算は
\(\vec{\ a\ }+\vec{\ b\ }=(a_1-b_1,a_2-b_2)\) で表されます。
3つの点 \(A,B,C\) を用いて \(\vec{AC}-\vec{AB}=\vec{BC}\) が成り立つという性質もあります。
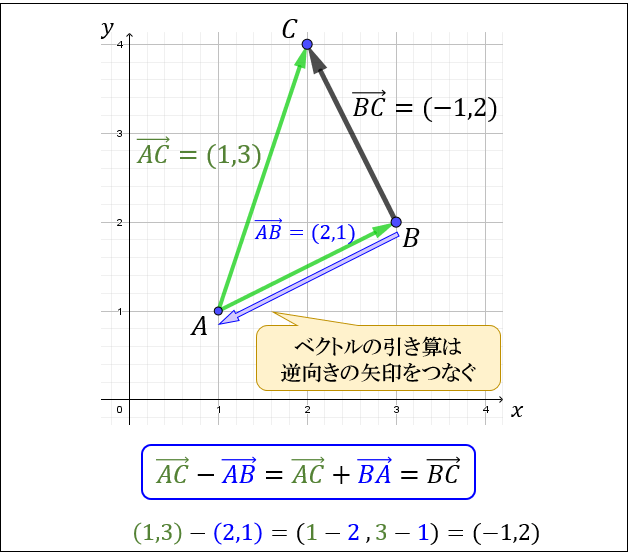
これは、\(-\vec{AB}=\vec{BA}\) より
\(\vec{AC}-\vec{AB}=\vec{AC}+\vec{BA}=\vec{BC}\) で導かれます。