フィボナッチ数列は「隣り合う2つの数を合計すると次の数になる数列」です。
英語では Fibonacci Sequence. 名前の由来は数学者レオナルド・フィボナッチより
具体的に書き並べていくと \(1,1,2,3,5,8,13,21,34,55,\cdots\) という数列になります。
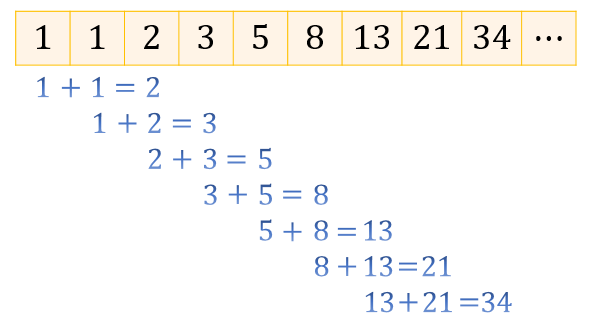
この数列を見ていくと
1番目の数と2番目の数の合計が3番目の数
2番目の数と3番目の数の合計が4番目の数
3番目の数と4番目の数の合計が5番目の数
となっていて、隣り合う2つの数を合計すると次の数になることが分かりますね。
このフィボナッチ数列に出てくる数は「フィボナッチ数」と呼ばれ
● ひまわりの種の並びは螺旋状に \(21,34,55\) 個となっている
● 多くの花の花びらの枚数は \(3,5,8,13,21\) 枚になっている
などなど、自然界で数多く見かける特殊な数となっています。
今回は、そんなフィボナッチ数列の性質を見ていきましょう。
フィボナッチ数列と黄金比の関係
フィボナッチ数列とは \(n\) 番目の数を \(F_n\) としたときに
\(F_{n+2}=F_{n}+F_{n+1}\) \((n\geqq1)\)
という漸化式で表わされる数列を指します。
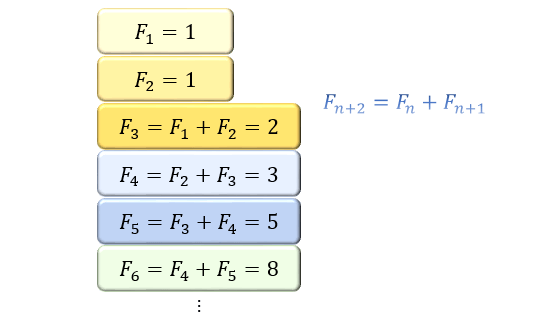
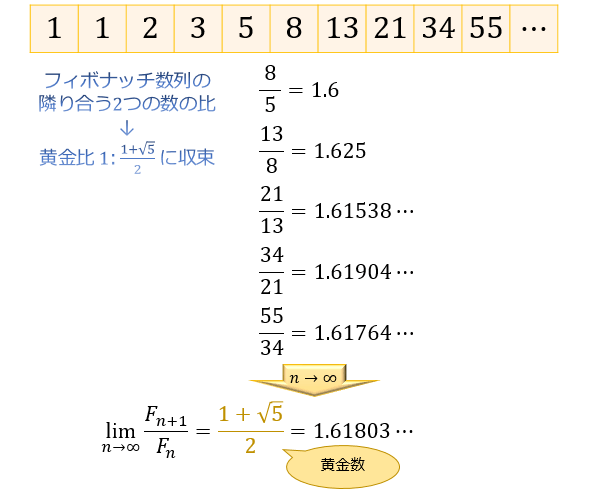
フィボナッチ数列は、最も美しい比とされる黄金比 $\displaystyle 1: \frac{1+\sqrt{5}}{2} $ と密接な関係にあります。
というのも、フィボナッチ数列の「隣り合う2つの数の比」はどれも黄金比に非常に近い値を取っており、\(n\) が大きくなるにつれて黄金比に収束するという性質があるのです。
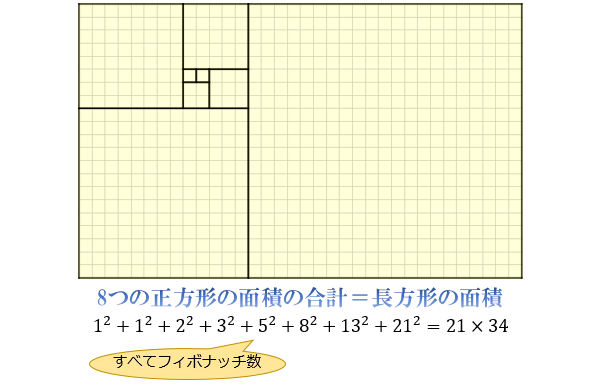
正方形の合計がフィボナッチ数の長方形
フィボナッチ数列には、その各項を1辺とする正方形の面積の合計がフィボナッチ数の積になるという性質もあります。
\((F_1)^2+(F_2)^2+\cdots+(F_n)^2=F_n×F_{n+1}\)
数式だけ見るとピンと来にくいかもしれませんが、図形で見ると分かりやすいです。
ビネの公式の証明(一般項)
フィボナッチ数列の \(n\) 番目の数 \(F_n\) は、 \(n\) を用いた次の式で一般化することができます。
$\displaystyle F_n=\frac{1}{\sqrt{5}}\left\{\left(\frac{1+\sqrt{5}}{2}\right)^n – \left(\frac{1-\sqrt{5}}{2}\right)^n \right\}$
この式を「ビネの公式」と言います。
ビネの公式の証明(導出)法は以下の通り。

ビネの公式はパッと見は複雑な印象を受けますが、第2項は約\(-0.618\) の \(n\) 乗。つまり \(n\) が十分に大きければ \(0\) に収束するので、\(F_n\) は黄金数の \(n\) 乗の \(\frac{1}{\sqrt{5}}\) 倍に近似することができます。