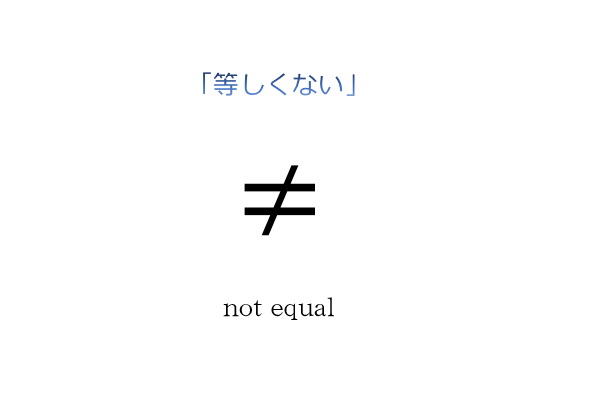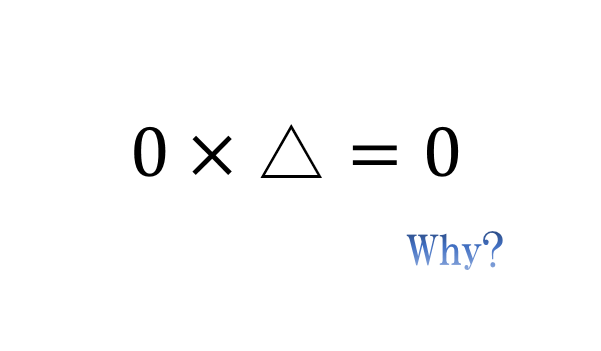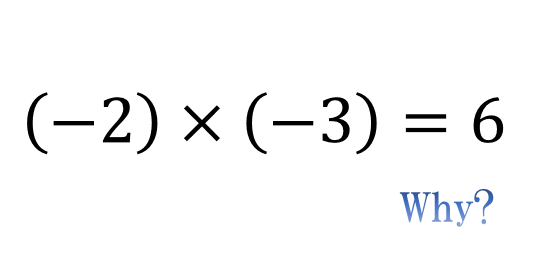
今回は、中学数学における最初の関門「正の数・負の数の計算問題」について。
皆さんは、「マイナス×マイナス=プラス」となる理由を身の回りの具体例を使って説明して欲しいと言われたらどう答えるでしょうか。
あらためて考えてみると、ぼくたちの身の回りではマイナスどうしのかけ算が行われるものはそう多くありません。
図形の面積:プラス×プラス
借金が倍に:マイナス×プラス
嫌な事と大変な事がかけ合わさる:マイナス+マイナス
マイナスどうしのかけ算を実生活で見かけることって、めったに無いですよね。
そのため、「なぜマイナス×マイナス=プラスになるのか」が直感的に理解しにくいという問題があります。
そこで今回は、「負の数どうしのかけ算が、なぜ正の数になるのか」を、図を使って説明していこうと思います。
負の数のかけ算が正の数になる理由
まず、「負の数どうしのかけ算が正の数になること」を数式上で実感してみましょう。
下の数式は、\((-2)\) にかける数を徐々に減らしていくと答えがどうなるかを表しています。

\((-2)×3=-6\) などの答えを見比べていくと
かける数が \(1\) 減るごとに答えが \(2\) ずつ増えているのが分かりますね。
では、かける数がさらに減っていき、ゼロを下回ったらどうなるのか?
ゼロを下回ったからと言って、数の法則が変わることはありません。
「マイナス×マイナス」も同じように、かける数が \(1\) 減るごとに答えが \(2\) ずつ増えていきます。
その結果「マイナス×マイナス」は \(0\) よりも大きい数、つまり正の数となるんです。
この数式の並びを見ると、なぜ「マイナス×マイナス」がプラスになるのかが、少し分かりやすくなったのではないでしょうか。
図を使った教え方
次は、具体例と図を使って「マイナス×プラス=マイナス」と「マイナス×マイナス=プラス」を見ていきましょう。
①マイナス×プラス=マイナス
今、あなたはお風呂の栓を抜いてお風呂のお湯を流しています。
午前 \(7\) 時現在、お湯は \(4\) リットル残っています。
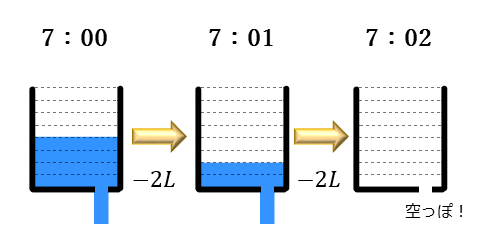
Q: \(1\) 分後にお風呂をみると、\(2\) リットルお湯が減っていました。
お湯の減る速度が一定とすると、午前 \(7\) 時 \(02\) 分にお湯はどれだけ残っているでしょうか?
A: \(1\) 分で \(2\) リットルお湯が減っていたということは、お湯の量は \((-2) [L/分]\) ずつ変動しているわけです。
そして午前 \(7\) 時 \(02\) 分は、「午前 \(7\) 時 \(00\) 分から見て \(2\) 分後」です。
ということは、午前 \(7\) 時 \(02\) 分のお湯の量は
\(4[L]+(-2)[L/分]×2[分]=4-4=0[L]\)
のこり \(0\) リットル。つまり空になったことになります。
午前 \(7\) 時 \(00\) 分以降におけるお湯の量を調べるときは「マイナス×プラス」の計算が役に立つ、というわけですね。
②マイナス×マイナス=プラス
では、午前 \(7\) 時 \(00\) 分以前におけるお湯の量はどうすれば求められるのか?
そこで役に立つのが、「マイナス×マイナス」の計算です。
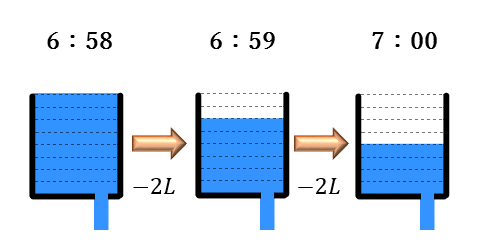
Q:午前 \(7\) 時現在、お湯は \(4\) リットル残っています。
お風呂のお湯が減る速度は一定で、\(1\) 分間に \(2\) リットル減ることが分かっています。
午前 \(6\) 時 \(55\) 分からお湯を抜いていたとして、午前 \(6\) 時 \(58\) 分にお湯はどれだけ残っていたでしょうか?
A:お湯の量の変動は \((-2)[L/分]\)
そして午前 \(6\) 時 \(58\) 分は、「午前 \(7\) 時 \(00\) 分から見て \((-2)\) 分後」です。
ということは、午前 \(6\) 時 \(58\) 分のお湯の量は
\(4[L]+(-2)[L/分]×(-2)[分]=4+4=8[L]\)
実際に図を見れば、\(8L\) 残っていることが分かりますよね。
このように「マイナス×マイナス」を利用することで、基準時間より前の時間におけるお湯の量を調べられるようになりました。
負の数のかけ算は、動画の逆再生
そう、つまりマイナス×マイナスというのは
「時間の経過とともに減っている『何か』が、時間を戻したときにどうなっているか?」
を求めるときに便利な計算式なんです。
「この \(2L\) は『増えた \(2L\) 』だっけ?この \(3\) 分は『 \(3\) 分戻った』だっけ?」といちいち考えなくても、増えるのはプラス・減るのはマイナスとおさえておけば、量の増減・時間の前後のすべてに対応できるようになる。
これこそが、「マイナス×マイナス=プラス」を勉強する最大のメリットです。
イメージとしては「後ろ向きに歩いている人の動画を逆再生してみると、前に進んでいるように見える」なんかが分かりやすいかもしれません。
分配法則を使った証明
最後に、分配法則 \(a×(b+c)=a×b+a×c\) と \(1+(-1)=0\) から \((-1)×(-1)=1\) を証明して、終わりにしたいと思います。