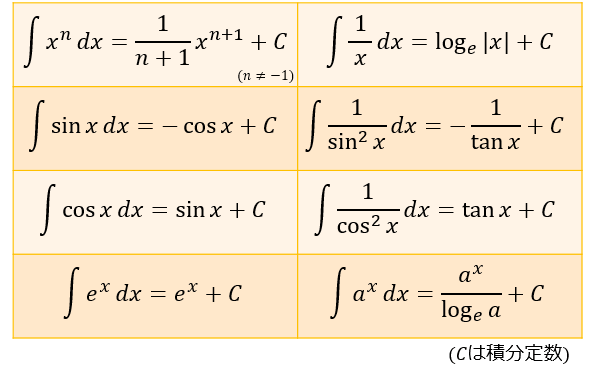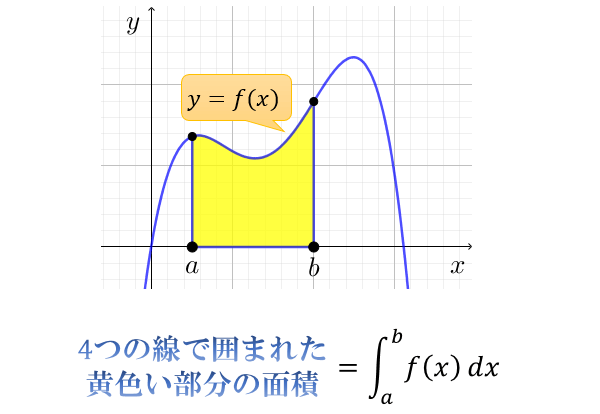
積分とは「微分の反対」に相当する操作で、関数 \(f(x)\) を使って囲まれた部分の面積を求めることを意味します。

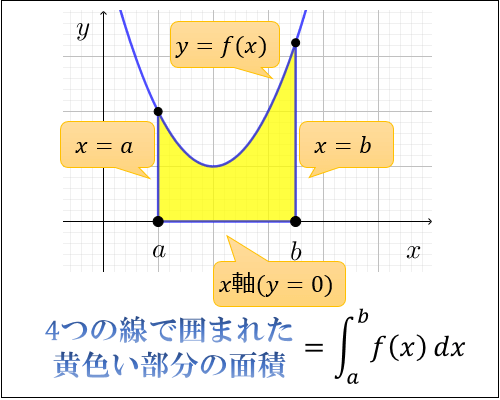
例えば $\displaystyle \int_a^b f(x) dx$ は「\(x\)軸 \(,y=f(x)\) \(,x=a\) \(,x=b\) で囲まれた部分の(符号付き)面積」を求めることを意味します。(ただし \(x\) 軸の下側にある部分の面積はマイナスとする)
今回は、具体例を通じて「積分の計算の意味」を見ていきましょう。
積分の計算と面積
例えば $\displaystyle \int_1^3 (x^2-3x+4) dx$ は、下図の黄色い部分の面積を求めることを意味します。
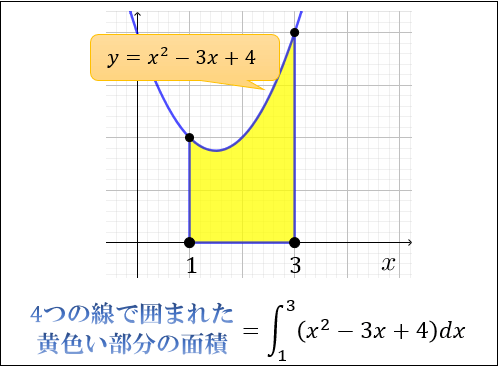
実際に計算してみると、$\displaystyle \int_1^3 (x^2-3x+4) dx=\dfrac{14}{3}$ と求まります。
(計算の仕方は積分のやり方と基礎公式。不定積分と定積分の違いとは?の記事を参照)
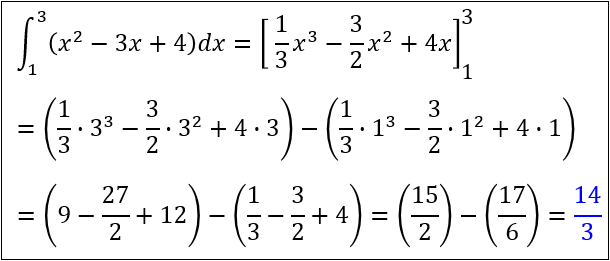
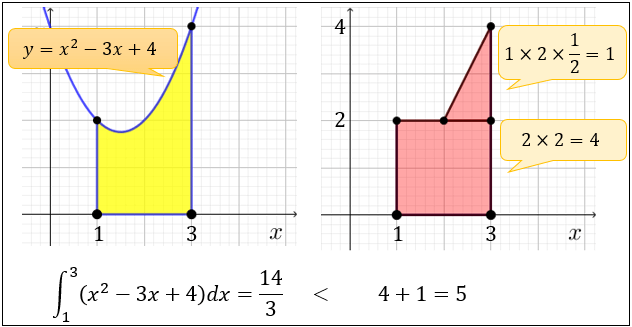
x軸の下側の部分の面積はマイナス
$\displaystyle \int_{-1}^3 (x^2-2x) dx$ は、下図の黄色い部分の面積から青い部分の面積を引いた値を求めることを意味します。
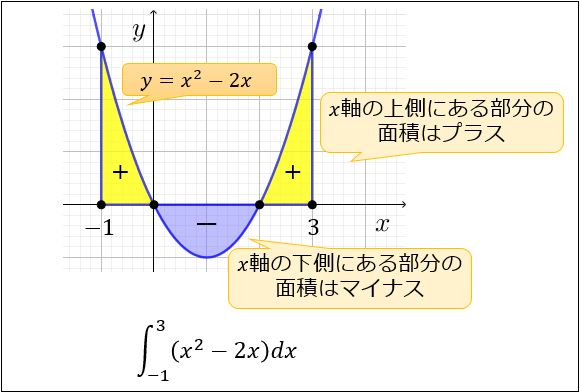
実際に計算してみると、$\displaystyle \int_{-1}^3 (x^2-2x) dx=\dfrac{4}{3}$ と求まります。
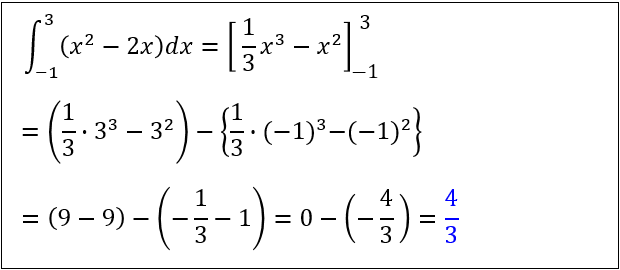
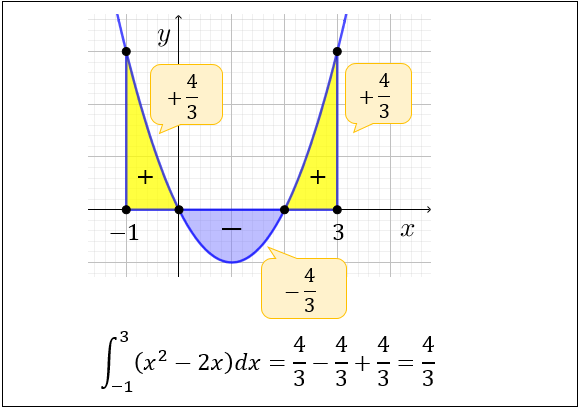
これは、2つの黄色い図形 \(4/3×2\) と青い部分 \(-4/3\) から成り立っています。
【まとめ】$\displaystyle \int_a^b f(x) dx$ は「\(x\)軸 \(,y=f(x)\) \(,x=a\) \(,x=b\) で囲まれた部分の符号付き面積」を求めることを意味する。(ただし \(x\) 軸の下側にある部分の面積はマイナスとする)
なぜ積分で面積が求まるのか?
さて、それではなぜ $\displaystyle \int_a^b f(x) dx$ が「\(x\)軸 \(,y=f(x)\) \(,x=a\) \(,x=b\) で囲まれた部分の符号付き面積」となるのでしょうか?
その答えは、「\(x\)軸 \(,y=f(x)\) \(,x=a\) \(,x=t\) で囲まれた部分の符号付き面積」を \(S(t)\) とおいて、\(t\) を少しずつ大きくしていくと分かります。
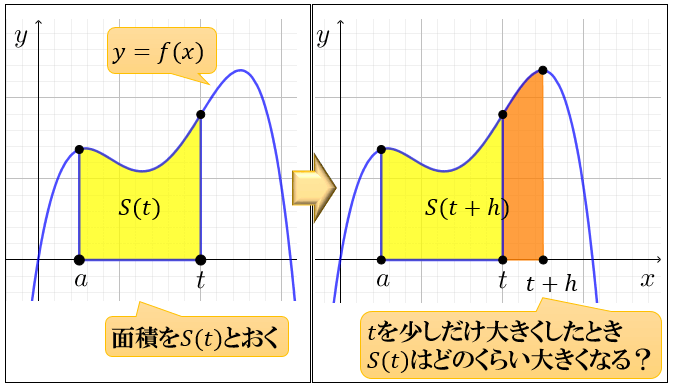
\(t\) を少しだけ大きくして \(t+h\) にしたとき、\(S(t)\) は \(S(t+h)-S(t)\) の分だけ大きくなります。
(図のオレンジ色の部分)
このオレンジ色の部分の面積は、明らかに「下図の青い部分より大きく」「下図の青+赤より小さい」ですよね。
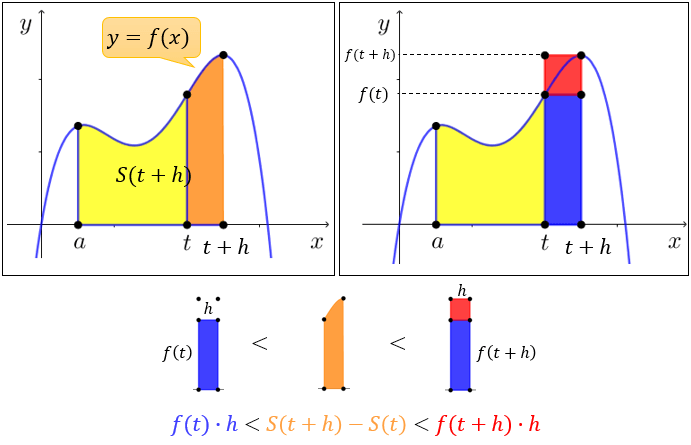
ここで、
青い部分の面積は \(f(t)×h\)
青+赤の面積は \(f(t+h)×h\)
であることから
\(f(t)×h<S(t+h)-S(t)<f(t+h)×h\)
が成立します。
あとは両辺を \(h\) で割り、極限をとってから「はさみうちの原理」を使うと
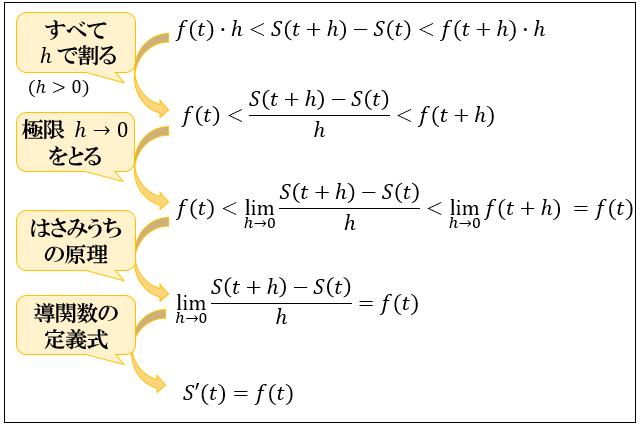
\(S(t)\) を微分した関数である \(S'(t)\) が \(f(t)\) と一致することが分かります。
あとは両辺を積分してから積分定数を計算すると
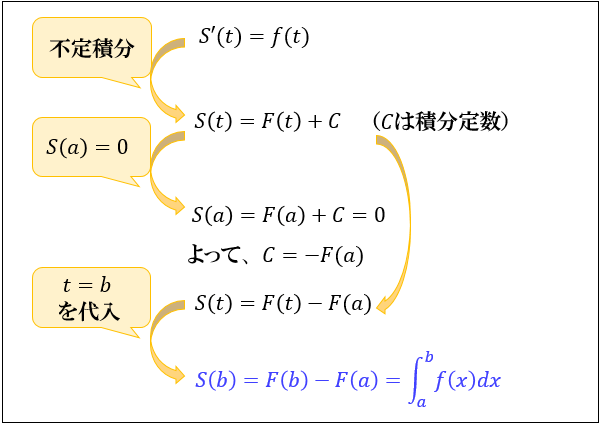
以上から
\(S(b)\) 、すなわち「\(x\)軸、\(y=f(x)\)、\(x=a\)、\(x=b\) で囲まれた部分の符号付き面積」
と
$\displaystyle \int_a^b f(x) dx$
が一致することが分かりました。
これが、$\displaystyle \int_a^b f(x) dx$ が「\(x\)軸、\(y=f(x)\)、\(x=a\)、\(x=b\) で囲まれた部分の符号付き面積」となる理由です。