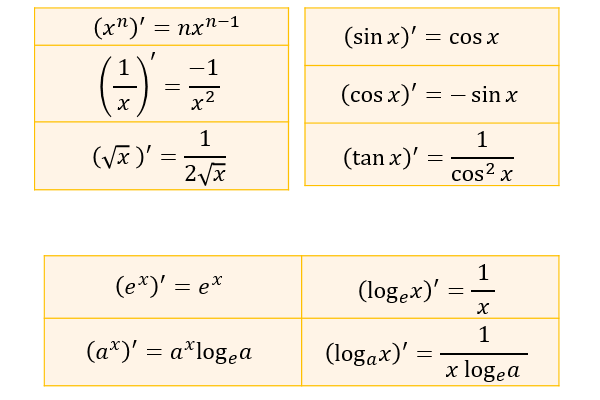関数 \(f(x)\) に対して、以下の式で表される導関数 \(f'(x)\) を求めることを「関数 \(f(x)\) を微分する」と言います。
$$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $$
【例題】関数 \(f(x)=3x^2\) を微分してください。
$$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\\=\lim_{h \to 0}\frac{3(x+h)^2-3x^2}{h}\\=\lim_{h \to 0}\frac{3(x^2+2xh+h^2)-3x^2}{h}\\=\lim_{h \to 0}(6x+3h)=6x $$
【答え】\(f'(x)=6x\)
微分について直感的に理解するのに使えるのが、速度という考え方です。
この記事では「速度」を通じて4つのステップから微分の仕組みを見ていきましょう。
微分がわかる4つのステップ

いま、地上から宇宙に向けて物体Aを発射しようとしています。
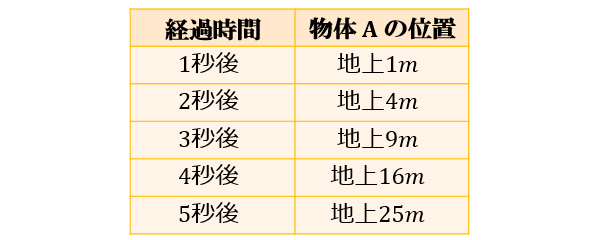
物体Aは、発射してから \(x\) 秒後に地上 \(f(x)=x^2\) m 地点を通過することが分かっています。
ここで、物体Aの \(x\) 秒後時点での速度を知りたい場合、どうやって求めれば良いでしょうか?
Step① 2秒間の平均速度
$$\displaystyle \frac{f(b)-f(a)}{b-a} $$
(\(a=3,b=5\))
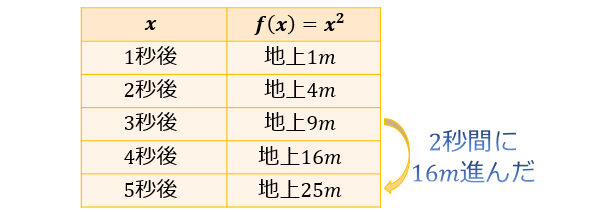
物体Aは、発射の \(3\) 秒後に地上 \(9\) m地点を通過し、\(5\) 秒後に地上 \(25\) m地点を通過します。
つまり、\(2\) 秒間に \(16\) m進むということですよね。
これを速度の公式\(「速度=距離÷時間」\)に当てはめると、「発射の \(3\) 秒後~ \(5\) 秒後」の平均速度は \(16÷2=8\) m/秒と求まります。
$$\displaystyle 変化の割合=\frac{f(5)-f(3)}{5-3}\\=\frac{25-9}{5-3}=8[m/秒] $$
Step② h秒間の平均速度
$$\displaystyle \frac{f(a+h)-f(a)}{h} $$
問2.物体Aの「発射の \(3\) 秒後」から「発射の \(3+h\) 秒後」までの平均速度は何m/秒か?
物体Aは、発射の \(x\) 秒後に地上 \(x^2\) m 地点を通過するわけですから、発射の \(3\) 秒後に地上 \(9\) m地点を通過し、\(3+h\) 秒後には地上 \((3+h)^2=9+6h+h^2\) m地点を通過します。
つまりは、\(h\) 秒間に \(6h+h^2\) m進むということになります。
これを速度の公式\(「速度=距離÷時間」\)に当てはめると、「\(3\) 秒後~ \(3+h\) 秒後」の平均速度は \(6+h\) m/秒だと分かります。
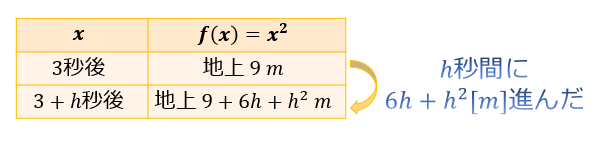
$$\displaystyle 変化の割合=\frac{f(3+h)-f(3)}{(3+h)-3}\\=\frac{(3+h)^2-9}{h}=\frac{(9+6h+h^2)-9}{h}\\=\frac{6h+h^2}{h}=6+h[m/秒] $$
さて、いま「発射の \(3\) 秒後」から「発射の \(3+h\) 秒後」までの平均速度が分かりました。
それではここで、この \(h\) を限りなく \(0\) に近づけていくと、何が求まるでしょうか?
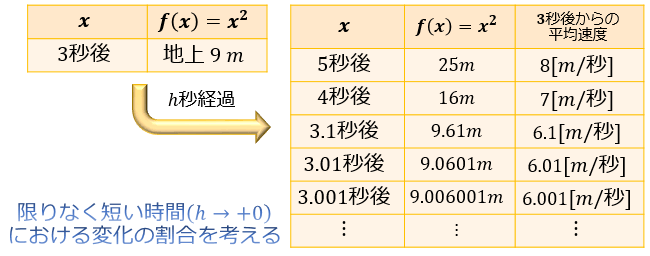
答えは、「発射の \(3\) 秒後」から「発射の \(3.000\cdots\) 秒後」までの平均速度。
すなわち、「発射の \(3\) 秒後」時点での瞬間的な速度を考えることができるようになります。
Step③ 3秒後の瞬間的な速度
$$\displaystyle f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h} $$
問3.物体Aの「発射の \(3\) 秒後」時点での瞬間速度は何m/秒か?
「発射の \(3\) 秒後~ \(3+h\) 秒後」の平均速度 \(6+h\) m/秒について、\(h\) を限りなく \(0\) に近づけると \(6+h→6\) m/秒。
ここから、「発射の \(3\) 秒後」時点での瞬間的な速度は \(6\) m/秒ということができます。
$$\displaystyle f'(3)=\lim_{h \to 0}\frac{f(3+h)-f(3)}{(3+h)-3}\\=\lim_{h \to 0}\frac{(9+6h+h^2)-9}{h}\\=\lim_{h \to 0}(6+h)=6[m/秒] $$
この瞬間的な変化の割合 \(f'(3)\) のことを「\(x=3\) における微分係数」と言います。
「発射の \(3\) 秒後」時点での瞬間的な速度を求められたら、次は「発射の \(1\) 秒後・ \(5\) 秒後・ \(7\) 秒後・ \(15\) 秒後」時点での瞬間的な速度についても考えてみましょう。
「ここまでの長い手順をまた1つ1つ計算していくのは面倒だな…」と感じる方もいるかもしれませんが、大丈夫。
1つ1つ計算する手間を省く便利な方法があります。
それが、「発射の \(x\) 秒後」時点での瞬間的な速度を \(x\) の関数として求めること。

「発射の \(x\) 秒後」時点での瞬間的な速度を \(x\) の関数として求めることができれば、その \(x\) の関数に \(x=1,5,7,15\) を代入するだけで各時点での瞬間的な速度をパッと求められるようになります。
Step④ x秒後の瞬間的な速度=微分する
$$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $$
問4.物体Aの「発射の \(x\) 秒後」時点での瞬間速度は何m/秒か?
それでは、「発射の \(x\) 秒後」時点での瞬間的な速度を \(x\) の関数としてまとめて計算してみましょう。
物体Aは、発射の \(x\) 秒後に地上 \(x^2\) m地点を通過し、\(x+h\) 秒後には地上 \((x+h)^2\) \(=x^2+2xh+h^2\) m地点を通過します。
つまりは、\(h\) 秒間に \(2xh+h^2\) m進むということです。
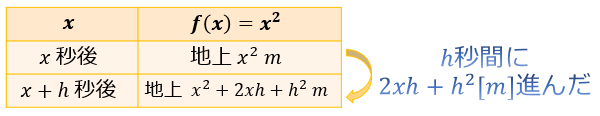
これを速度の公式に当てはめると「\(x\) 秒後~ \(x+h\) 秒後」の平均速度は \(2x+h\) m/秒
この \(h\) を限りなく \(0\) に近づけると、 \(2x+h→2x\) m/秒
よって、「発射の \(x\) 秒後」時点での瞬間的な速度は導関数 \(f'(x)=2x\) で表せることが分かります。
$$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{(x+h)-x}\\=\lim_{h \to 0}\frac{(x^2+2xh+h^2)-x^2}{h}\\=\lim_{h \to 0}(2x+h)=2x[m/秒] $$
導関数 \(f'(x)=2x\) の \(x\) に値を代入するだけで、好きな時点での瞬間的な速度を求められるようになったわけです。
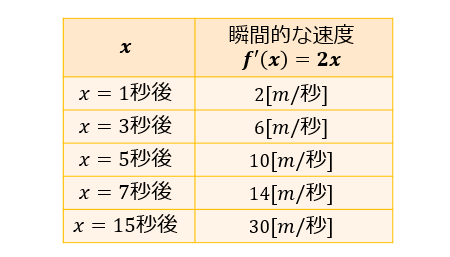
以上のように、「瞬間的な変化の割合 \(f'(x)\) を求めること」。
それが、微分の意味するところなんです。
微分する=導関数を求める=瞬間的な変化の割合を求める

日々変化しつづける経済・社会問題において
「瞬間的な変化の割合がプラスからマイナスに切り替わる瞬間」
「瞬間的な変化の割合がもっとも大きい瞬間」
を知りたいというケースは少なくありません。
微分はそんな要望にビシッと答えてくれる、応用範囲の広いツールとなっています。