トレミーの定理とその証明。向かい合う2組の辺と対角線の関係性

 

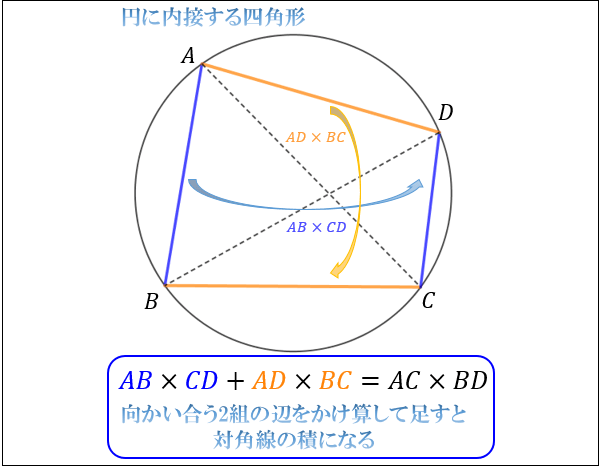
円に内接する四角形 \(ABCD\) には「向かい合う2組の辺をかけ算して足すと、対角線の積と等しくなる」という性質があります。

これを、トレミーの定理と言います。

 

 

このページでは、このトレミーの定理の証明と使い方を解説していきます。

 

トレミーの定理の証明

トレミーの定理の証明には、余弦定理を使います。

 

 

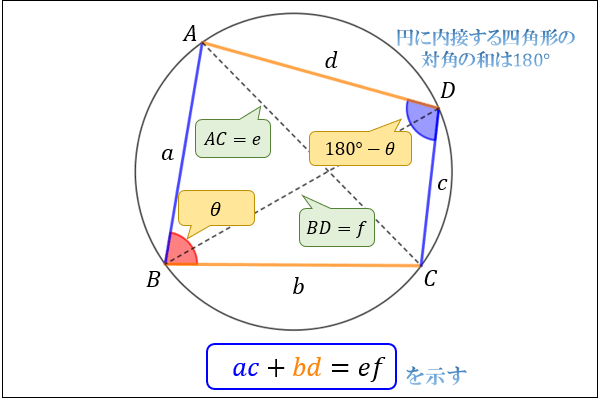
まず初めに、\(∠B=θ\) とおきます。

 

すると、円に内接する四角形の性質から「対角の和は \(180°\)」なので、\(∠D=180°-θ\) だと分かりますね。

 

次に、三角形 \(ABC\) と三角形 \(ADC\) について余弦定理を用いると

● \(\cos{θ}=\dfrac{a^2+b^2-e^2}{2ab}\) 

● \(\cos{(180°-θ)}=\dfrac{c^2+d^2-e^2}{2cd}\)

という2つの等式が成り立つことが分かります。

 

ここで、三角関数の性質 \(\cos{(180°-θ)}=-\cos{θ}\) で \(2\) つの等式をつなげると…

 

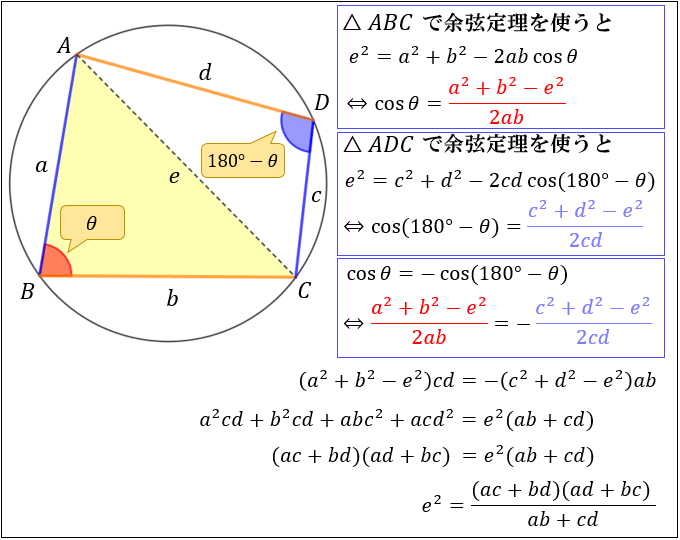
\(e^2=\dfrac{(ac+bd)(ad+bc)}{ab+cd}\)

が求まります。

 

次に、これと同じことを三角形 \(BAD\) と三角形 \(BCD\) についても計算します。

 

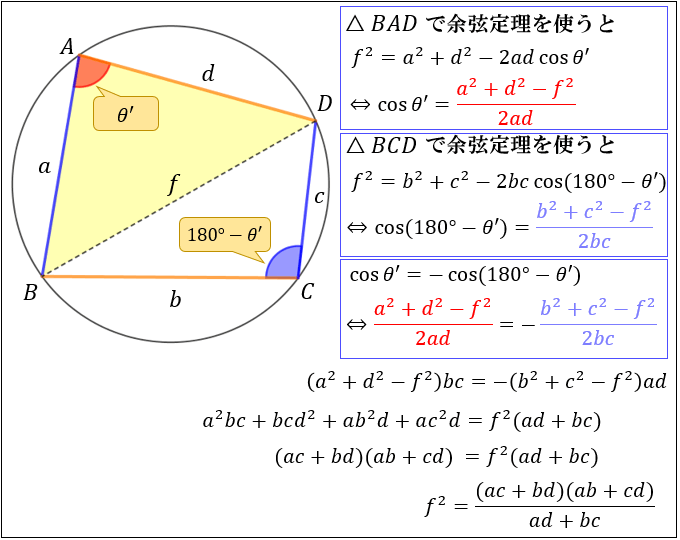
すると

\(f^2=\dfrac{(ac+bd)(ab+cd)}{ad+bc}\)

が求まります。

 

最後に、\(e^2\) と \(f^2\) をかけ算してから平方根をとると

 

「向かい合う2組の辺をかけ算した合計 \(ac+bd\)」が「対角線の積 \(ef\)」と等しいことを示せました。

 

トレミーの定理を使った例題

 

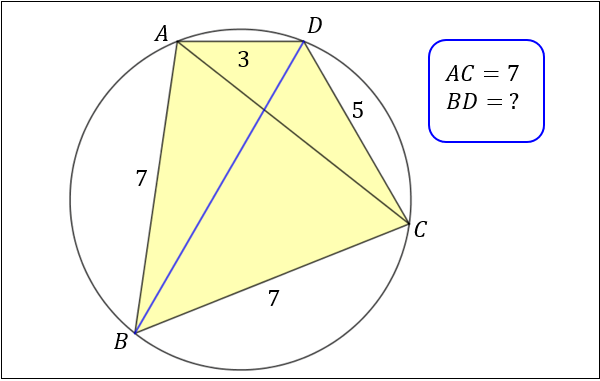
\(AB×CD+AD×BC=AC×BD\) なので

\(7×5+3×7=7×BD\) となり、\(BD=8\) と求まります。