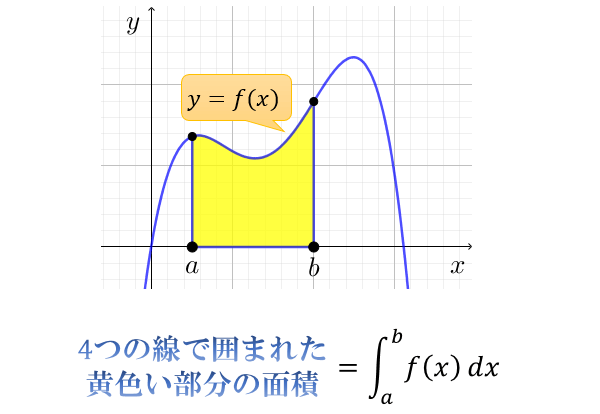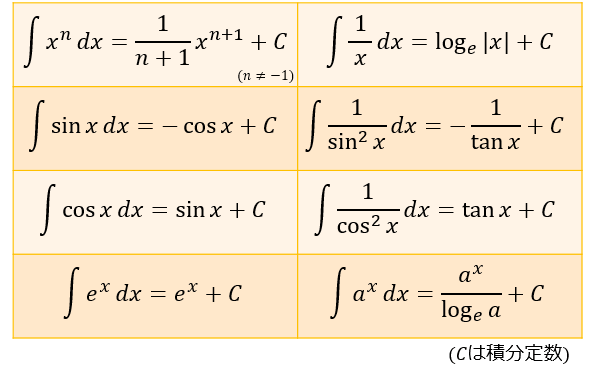
このページでは、よく使う積分の公式をまとめています。
積分の公式は、微分の公式をひっくり返して考えると覚えやすいです。
xのn乗の積分公式
● $\displaystyle \int x^n dx=\dfrac{1}{n+1}x^{n+1}+C$ \((n≠-1)\)
● $\displaystyle \int {\dfrac{1}{x}} dx=\log_e{|x|}+C$ \((n=-1)\)
【\(C\) は積分定数】
最も基本となる公式。
\(n=0,1,2\cdots\) だけでなく \(n=\dfrac{1}{2},-\dfrac{1}{2},-2\) も重要

三角関数の積分公式
● $\displaystyle \int \sin{x}\ dx=-\cos{x}+C$
● $\displaystyle \int \cos{x}\ dx=\sin{x}+C$
● $\displaystyle \int \dfrac{1}{\cos^2{x}}\ dx=\tan{x}+C$
● $\displaystyle \int \dfrac{1}{\sin^2{x}}\ dx=-\dfrac{1}{\tan{x}}+C$
タンジェントの積分にも公式があるが、重要度は低め
● $\displaystyle \int \tan{x}\ dx=-\log_e{|\cos{x}|}+C$
指数関数の積分公式
● $\displaystyle \int e^xdx=e^x+C$
● $\displaystyle \int a^xdx=\dfrac{a^x}{\log_e{a}}+C$ \((a>0,a≠1)\)
\(e≒2.718\) はネイピア数
対数関数の積分公式
● $\displaystyle \int \log_e{x}\ dx=x\log_e{x}-x+C$
\(\log_{e}{x}\) は自然対数。\(\log{x}\) と省略表記されることが多い>>対数の省略表記について
部分積分(不定積分・定積分)
● $\displaystyle \int f(x)g'(x)dx$
$\displaystyle=f(x)g(x)-\int f'(x)g(x)dx$
● $\displaystyle \int_a^b f(x)g'(x)dx$
$\displaystyle=\left[f(x)g(x)\right]_a^b-\int_a^b f'(x)g(x)dx$
例:$\displaystyle \int x\sin{x} \ dx$ の場合。\(f(x)=x\)、\(g(x)=-\cos{x}\) を代入する
\(f'(x)=1\)、\(g'(x)=\sin{x}\) となる点に注目
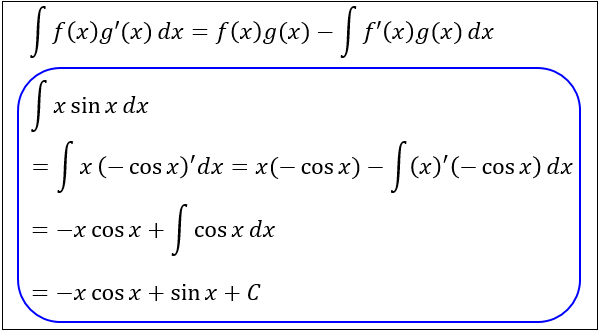
ガウス積分
● $\displaystyle \int_{-∞}^{∞} e^{-ax^2}dx=\sqrt{\dfrac{π}{a}}$ \((a>0)\)