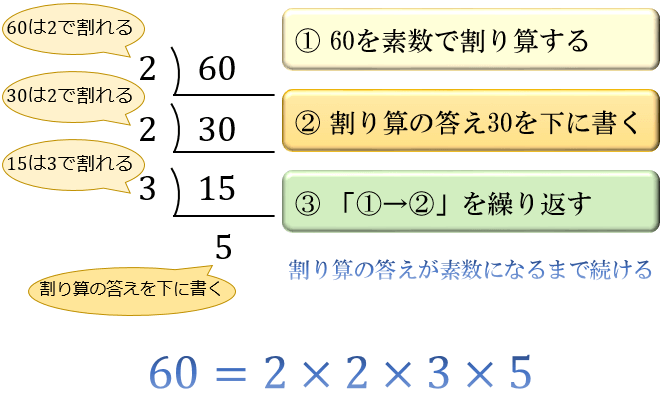
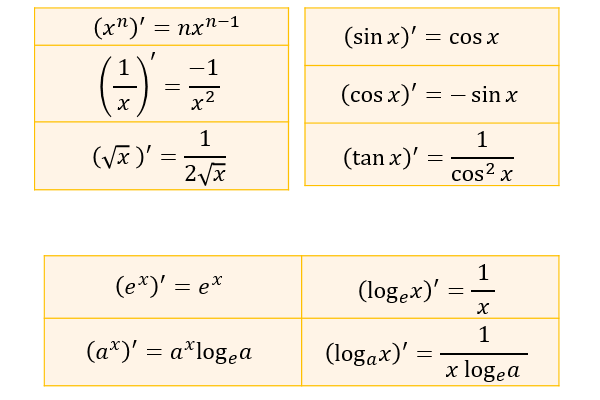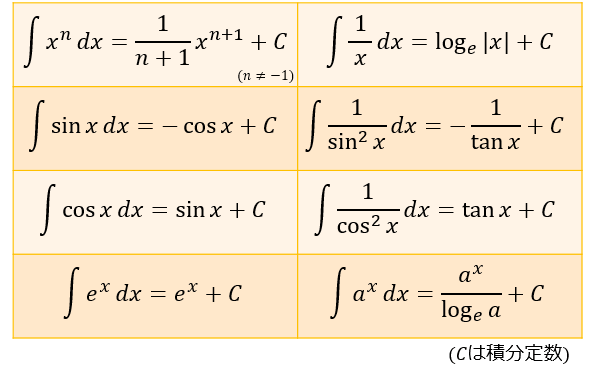関数 \(f(x),g(x)\) とそれらを微分した \(f'(x),g'(x)\) に対して成立する以下の公式を、部分積分と言います。
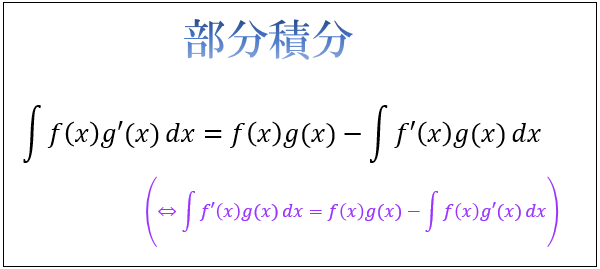
(英語では Integration by parts)
例えば $\displaystyle \int x \sin{x}\ dx$ を計算してみましょう。
この場合
「\(f(x)=x\) を微分したら \(f'(x)=1\) になる」
「\(g'(x)=\sin{x}\) を積分したら \(g(x)=-\cos{x}\) になる」
を当てはめると、以下のように部分積分できます。
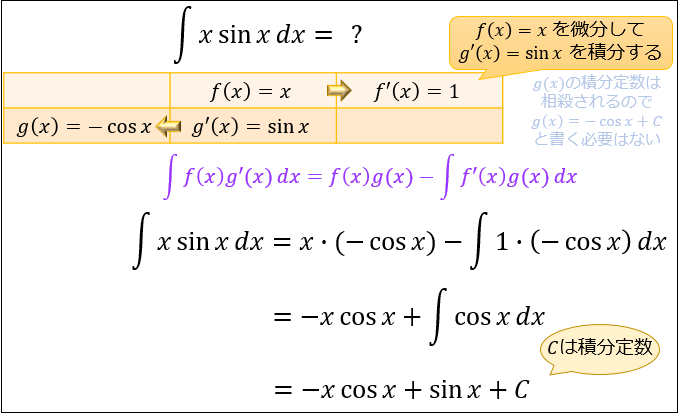
今回は、部分積分のやり方とそのコツについて書いていきます。
部分積分の考え方。どっちを微分すれば良いのか?
部分積分は
① 積分したい関数が「2つの関数のかけ算 \(f(x)g'(x)\) 」である
② 2つの関数の一方 \(f(x)\) を微分した \(f'(x)\) がカンタンな関数である( \(f'(x)=1\) など)
という2つの条件を満たすときに有効なテクニックです。
2つの関数の一方をカンタンな関数に変換することで、積分の計算をしやすくするのが部分積分のねらいです。

部分積分をするときは
微分したら元よりカンタンな関数になる方を \(f(x)\)
積分してもあまり複雑な関数にならない方を \(g'(x)\)
と置くのがコツです。
実際に、いくつか例題を解いてみましょう。
部分積分問題
① \(x\) と指数関数
問①.$\displaystyle \int xe^x\ dx$ を求めて下さい。
2つの関数 \(x\) と \(e^x\) のかけ算なので、部分積分を使います。
微分したら元よりカンタンになるのは \((x)’=1\) なので、\(f(x)=x\)
積分してもあまり複雑にならないのは \(\int e^x dx=e^x\) なので、\(g'(x)=e^x\)
これを部分積分の公式に当てはめると、以下のように求まります。

② \(x\) と三角関数
問②.$\displaystyle \int x\cos{2x}\ dx$ を求めて下さい。
微分したら元よりカンタンになるのは \((x)’=1\) なので、\(f(x)=x\)
積分してもあまり複雑にならないのは \(\int \cos{2x}\ dx=\dfrac{\sin{2x}}{2}\) なので、\(g'(x)=\cos{2x}\)
これを部分積分の公式に当てはめると、以下のように求まります。
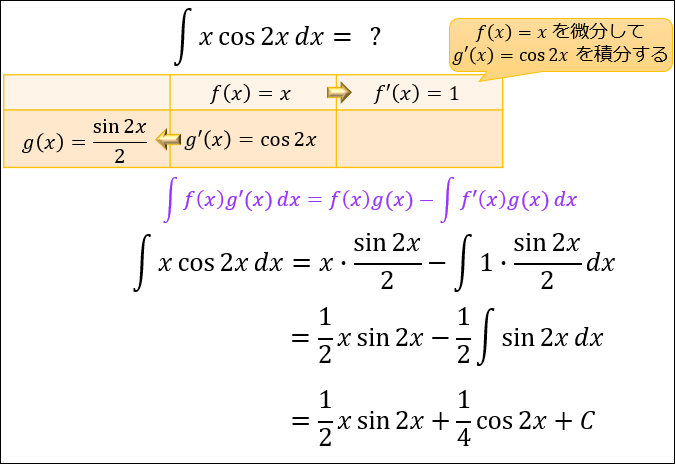
③ 対数関数
問③.$\displaystyle \int \log_e{x}\ dx$ を求めて下さい。
積分の公式を暗記しておけば解けますが、自信がないときは部分積分を使うと確実です。
ここでは、\(\log_e{x}=1×\log_e{x}\) と考えるのがコツ。
微分したら元よりカンタンになるのは \((\log_e{x})’=\dfrac{1}{x}\) なので、\(f(x)=\log_e{x}\)
積分してもあまり複雑にならないのは \(\int 1\ dx=x\) なので、\(g'(x)=1\)
これを部分積分の公式に当てはめると、以下のように求まります。
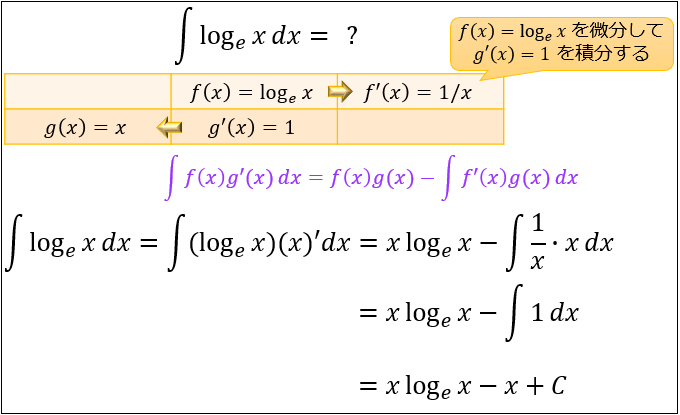
積分に回す優先順位
2つの関数のどちらを積分する関数 \(g'(x)\) とおくべきか迷うという場合は、以下の優先順位で考えると分かりやすいです。

この表の優先順位を見ると
問①.$\displaystyle \int xe^x\ dx$ は \(e^x\) を積分
問②.$\displaystyle \int x\cos{2x}\ dx$ は \(\cos{2x}\) を積分
問③.$\displaystyle \int \log_e{x}\ dx$ は \(1=x^0\) を積分。つまり \(\log_e{x}\) を微分
で部分積分できることが分かります。
次のページでは部分積分の証明と「部分積分をくり返すパターン」の問題を見ていきましょう。