このページでは、平行四辺形でも台形でもひし形でもない「ただの四角形」の面積の求め方をまとめています。
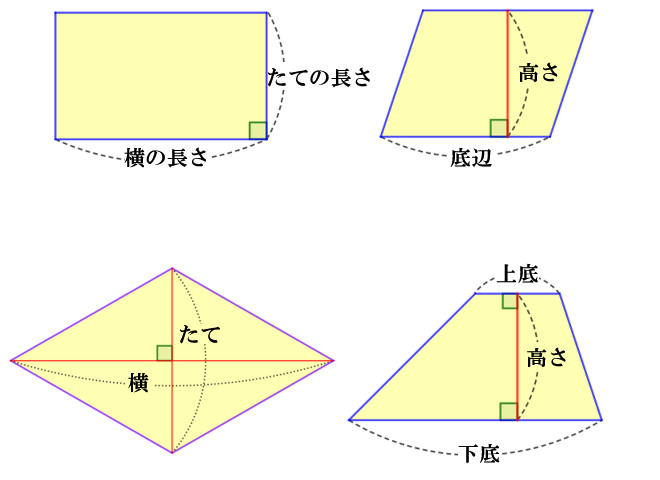
平行四辺形・台形・ひし形などの面積の求め方については「四角形の面積の求め方。公式とその仕組み【小学算数】」の記事で解説しています。
① 4つの辺と対角線の長さから求める
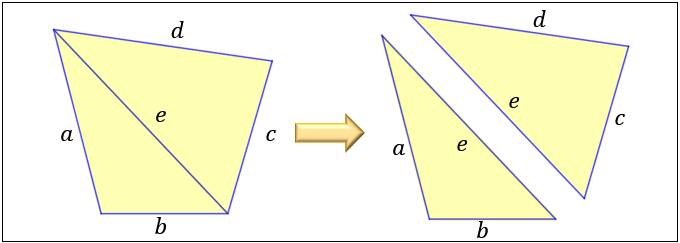
四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。
四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。
【ヘロンの公式】
3辺の長さ \(a,b,c\) が分かっている場合、その三角形の面積 \(S\) は
\(S=\sqrt{s(s-a)(s-b)(s-c)}\)
\(\left(ただし、s=\dfrac{a+b+c}{2}\right)\)
で求められる。

【例題】4つの辺 \(AB=6,BC=4,\) \(CD=5,DA=7,\) 対角線 \(AC=8\) の四角形 \(ABCD\) の面積を求めてください。

ヘロンの公式を2回使うことで、四角形の面積が
\(3\sqrt{15}+10\sqrt{3}\)
と求まりました。
② 2本の対角線の長さとその交わる角度から求める
2本の対角線の長さ \(a,b\) と対角線の交わる角度 \(θ\) が分かっている場合、その四角形の面積 \(S\) は
\(S=\dfrac{1}{2}ab \sin{θ}\)
で求められます。

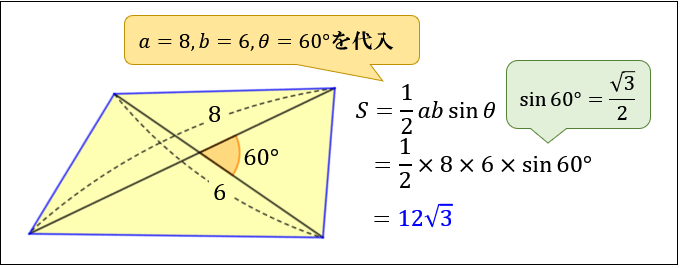
たとえば、「2本の対角線の長さが \(8,6\)、対角線の交わる角度が \(60°\) の四角形」の面積は
\(S=\dfrac{1}{2}×8×6×\sin{60°}=12\sqrt{3}\)
となります。
③ ブレートシュナイダーの公式で求める
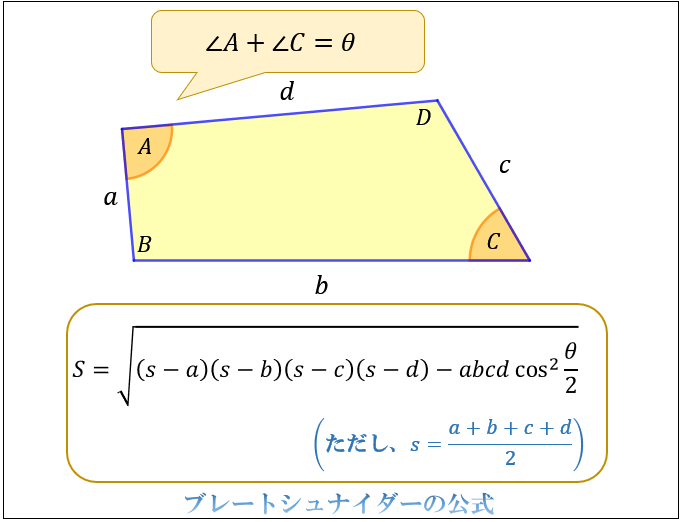
4辺の長さ \(a,b,c,d\) と対角の和 \(∠A+∠C=θ\) が分かっている場合、その四角形 \(ABCD\) の面積は、以下のブレートシュナイダーの公式から求めることができます。
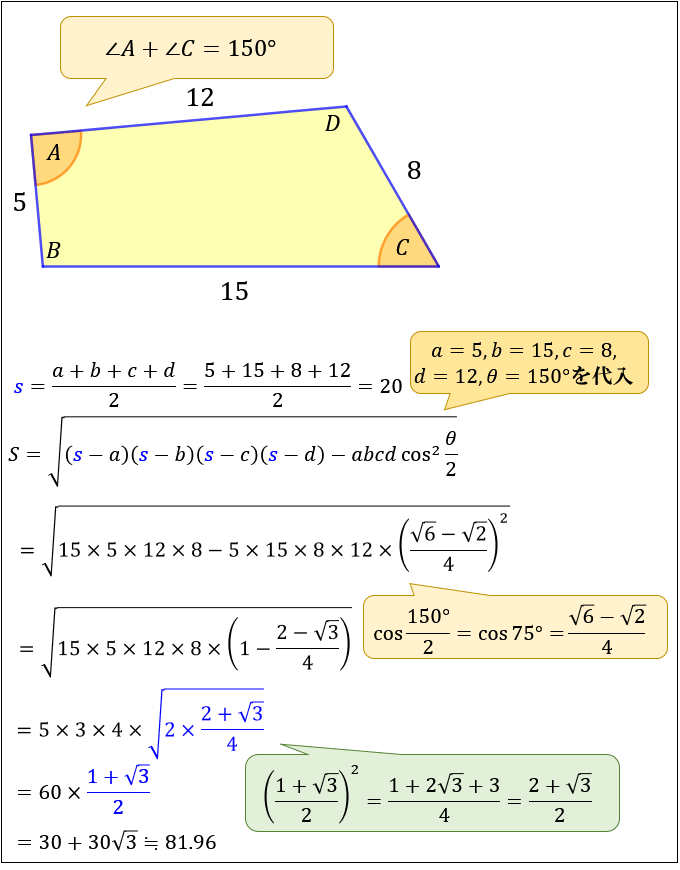
たとえば、「4辺の長さがそれぞれ \(5,15,\) \(8,12\) で1組の対角の和が \(150°\) の四角形」の面積は、ブレートシュナイダーの公式を使うことで
\(30+30\sqrt{3}≒81.96\)
と求まります。
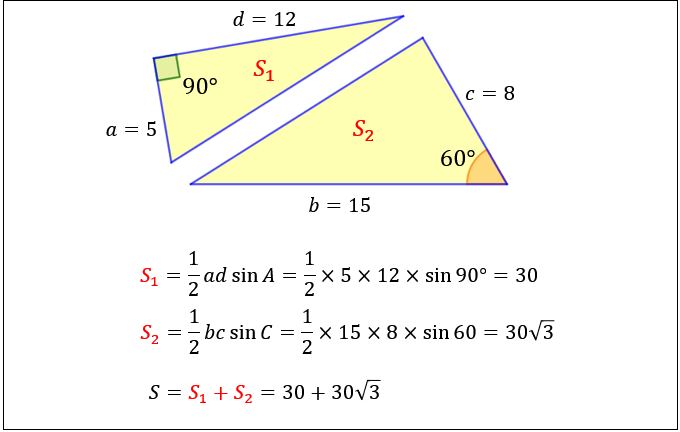
ただし、\(∠A\) と \(∠C\) の角度がそれぞれ分かっている場合は、三角形の面積の公式を利用して
\(S=\dfrac{1}{2}ad\sin{A}+\dfrac{1}{2}bc\sin{C}\)
から計算したほうが、楽に求められます。