部分分数分解とは「分数のかけ算を分数の足し算(引き算)に変形すること」を指します。
例えば、\(\dfrac{1}{20}=\dfrac{1}{4×5}\) は
\(\dfrac{1}{4×5}=\dfrac{1}{4}-\dfrac{1}{5}\) と変形できますよね。
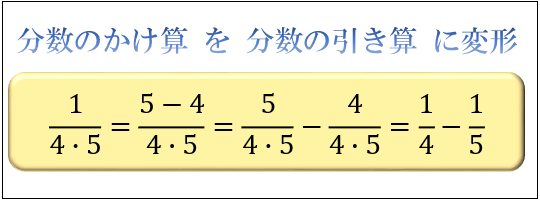
この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。
微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。
部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッと少なくなってきます。
ぜひ、ここで部分分数分解のコツをおさえていってください。
部分分数分解の公式
部分分数分解で「分数のかけ算を分数の足し算に変形する」には
いくつかのパターンを形で覚えておくと便利です。

まずは、主要な3つのパターンを具体例を通じてみていきましょう。
①1/(x+a)(x+b)の公式
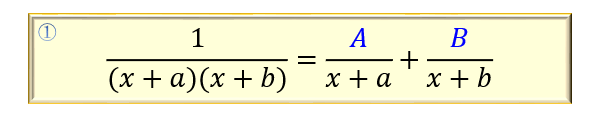
まずは、最もシンプルなパターン。
問①.\(\dfrac{1}{(x-2)(x+1)}\) を部分分数分解してください。
公式の形を覚えて、\(A,B\) がどんな条件を満たせば恒等式が成立するかを考えるのがコツです。

※恒等式とは:変数 \(x\) がどんな値でも常に成り立つ等式のこと
\(2x+5=ax+b\) が恒等式であるためには、\(a=2\ ,\)\(b=5\) である必要がある
②(px+q)/(ax+b)(cx+d)の公式

①の式をより一般化した形。
難しくなったように見えますが、計算の仕方は①とまったく同じです。
問②.\(\dfrac{2x+1}{(2x-3)(x+2)}\) を部分分数分解してください。

\(A+2B=2\) を2倍して \(2A+4B=4\) にしてから \(2A-3B=1\) で両辺を引くと
\(7B=4-1=3\) ⇔ \(B=\dfrac{3}{7}\) が求まり、 それを \(A+2B=2\) に代入すると
\(A=\dfrac{8}{7}\) も求まります。
③分母が二乗の公式
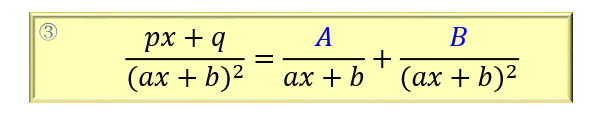
さて、今度は分母が2乗になっているパターンです。
問③.\(\dfrac{4x-1}{(2x+1)^2}\) を部分分数分解してください。

より複雑なパターン
ここまでの3つのパターンに慣れてきたら、より難しいパターンの部分分数分解に挑戦してみましょう。

このタイプの問題では、\(x\) に適当な数字を代入して \(A,B,C\) の関係式をよりカンタンにするのがコツです。
④3つに分かれる公式
問④.\(\dfrac{1}{(x+1)^2(x-3)}\) を部分分数分解してください。

⑤分母が1次式と2次式の積の公式
問⑤.\(\dfrac{2x+3}{(x+1)(x^2-x-1)}\) を部分分数分解してください。