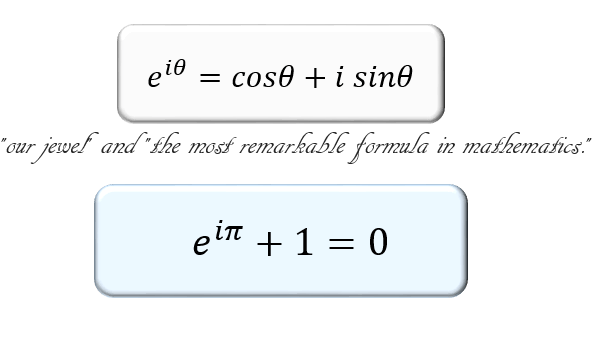突然ですが、皆さんは「ネイピア数 e (≒2.718)の \(0.1\) 乗」がいくつか分かりますか?
では、\(\sin{0.1}\) はどうでしょう?
パッと答えるのは難しいですよね。
数の世界にはこのように、指数関数・三角関数など計算が複雑な関数が少なくありません。
そのため、物理学や統計学の領域では「式が複雑になりすぎて、厳密な計算をするのが困難。近似的な式でいいから、計算をカンタンにする手法が欲しい」と感じることがあります。
そんなときに重宝する、便利なテクニック。それが、テイラー展開です。
photo credit:jphilipg
テイラー展開とは?
テイラー展開とは、関数 \(f(x)\) を多項式で近似する手法です。
①関数 \(f(x)\) が \(x=a\) を含むある区間で無限回微分可能
②テイラーの定理における剰余項 \(R_n\) が \(n→∞\) のとき \(0\) に収束する
という条件下において、\(f(x)\) は以下のような無限級数で表すことができます。
この式のことを、「\(f(x)\) の \(a\) を中心としたテイラー展開」と言います。

※ \(k!\) :\(k\) の階乗
テイラー展開は、\(a=0\) の場合について語られることが多く、この「\(f(x)\) の \(0\) を中心としたテイラー展開」のことを特にマクローリン展開と呼びます。

覚えておくと便利なマクローリン展開
たとえば、指数関数や三角関数といった難解な関数は、テイラー展開・マクローリン展開を使えば一気に計算が楽になります。
実際に、先ほどのマクローリン展開の式を \(e^x\) , \(\sin{x}\) , \(\cos{x}\) に当てはめたのが以下の式です。
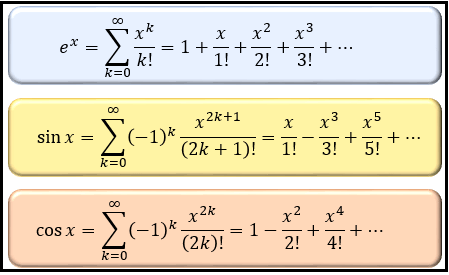
これら3つは使うことが多いので、できれば暗記しておきたいところです。
それでは、このマクローリン展開を使って、 \(e^{0.1}\) と \(\sin{0.1}\) をササっと求めてみましょう。
ここでのコツは、\(x^4\) 以降の項をすべて切り捨ててしまうことです。
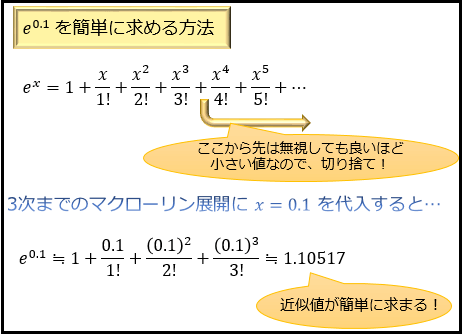
なぜ切り捨てても良いのかというと、\(x=0.1\) といったように小さな値であれば、\(x^4\)や\(x^5\)の項が「無視しても問題ないほど小さな値」になるからです。
実際に \(e^{0.1}\) や \(\sin{0.1}\) の正確な値と見比べると、\(x^3\) の項までのマクローリン展開が非常に精度の高い近似値になっていることが分かります。

一見すると複雑な式に見えたテイラー展開も、実際に計算してみると「関数をシンプルにする便利なテクニック」であることが実感できたのではないでしょうか。
他にも、\(\sin{1}=0.84147\cdots\) を求めるときは、7次までのマクローリン展開が精度の高い近似値になります。ぜひ一度計算して確かめてみてください
近似以外の使い方
テイラー展開・マクローリン展開は、近似する以外にも色々な使い道があります。
例えば、「〇分で平均△回起きる現象が、◇分で☆回起きる確率」を表す分布であるポアソン分布の期待値・分散を求めるときなどにも重宝します。
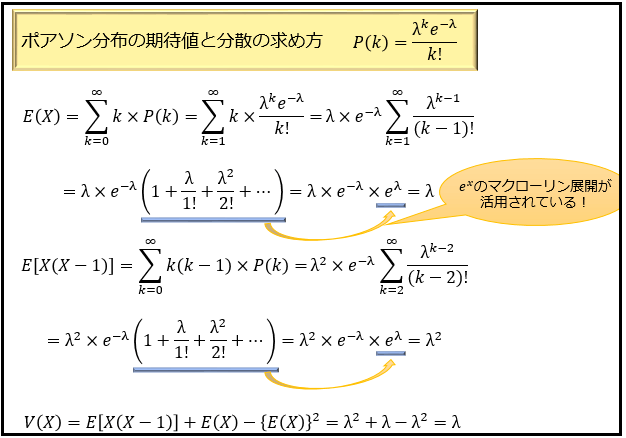
一度理解しておけば非常に使いやすい便利なテクニックなので、ぜひ覚えておきたいですね。