行列(Matrix)とは、数字・記号・式などを縦と横に並べたもののことを言います。

行列は、3次元以上の変数データを一括で処理するのに便利なツールです。
大量のデータを収集・解析しやすくなった現代において、行列の重要性は増していく一方。
今回は、そんな行列の基本事項とその有用性について軽く解説していきます。
行と列の考え方
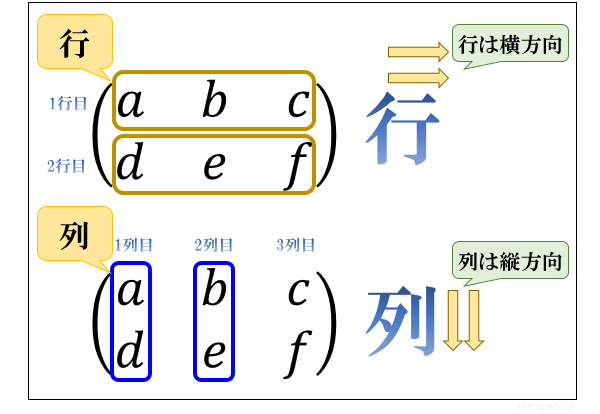
行列では
横方向の並びのことを「行」
縦方向の並びのことを「列」
と呼びます。
また、
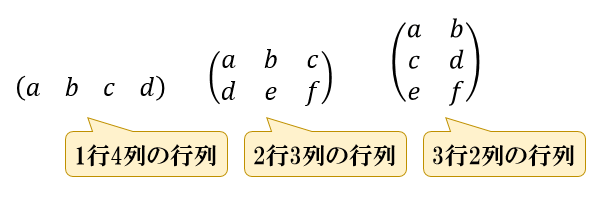
行列を構成する数字1つ1つを「成分」
行が \(m\) ・列が \(n\) の行列を「\(m\) 行 \(n\) 列の行列」
と言います。
行列の足し算・引き算
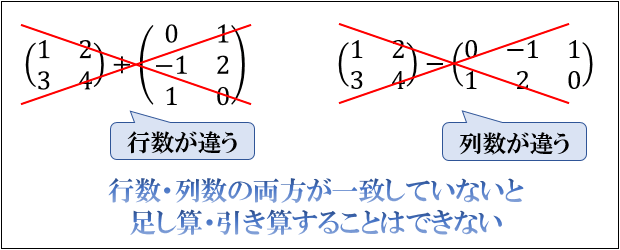
行列の足し算・引き算は、同じ行・同じ列の成分どうしを足し引きして計算します。

対応する成分がすべてそろっている必要があるため、行数と列数がそれぞれ一致する行列どうしでないと足し算・引き算することはできません。
行列のスカラー倍
行列には、1つの数(スカラー)をかけ算することができます。
これを「行列のスカラー倍」と言います。
行列を \(n\) 倍すると、行列の各成分すべてが \(n\) 倍されることになります。

行列のかけ算
行列は、行列どうしでかけ算することもできます。
行列の積は、左の行列の「行」と右の行列の「列」の組の同じ順番の数どうしの積を合計することで求まります。

このように、行列の積は「左 or 右」で計算の仕方が変わってくるので
2つの行列 \(A\) と \(B\) に対して、 \(A×B\) と \(B×A\) は必ずしも一致しません。
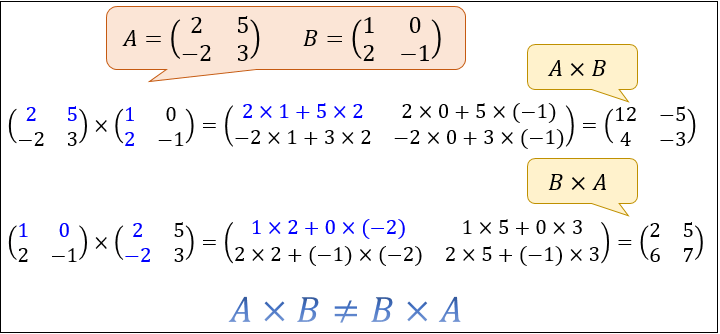
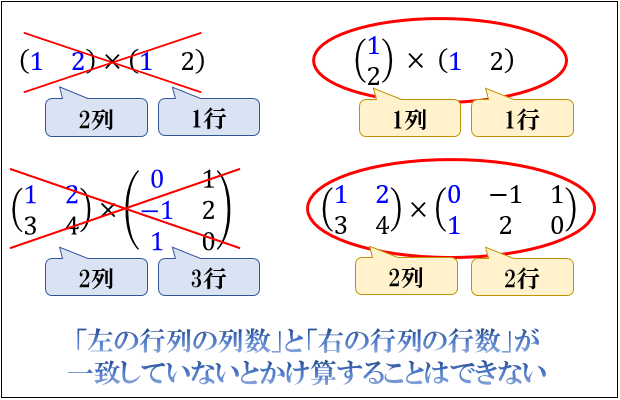
また、対応する成分がすべてそろっている必要があるため、「左の行列の”列”数」と「右の行列の”行”数」が一致していないと2つの行列をかけ算することはできません。
行列のかけ算のやり方については、以下の記事でくわしく解説しています。
行列は使い勝手がすごく良い!
さて、ここまで行列の計算方法を見てきました。
しかし、なぜわざわざこんな計算をする必要があるのでしょうか。
行列というものを用意し、その足し算・引き算・かけ算を定義して、どんなメリットがあるのか?
その答えは、「多元連立方程式を1本の式で表現・計算できる」ことにあります。
たとえば、以下の3つの連立方程式。
この連立方程式の解 \(x_1,x_2,x_3\) を求めようとしたら、本来は多くの式を書きならべる必要がありますが、行列であれば \(AX=B\) という1つの式で表し、一発で解を求めることができるのです。
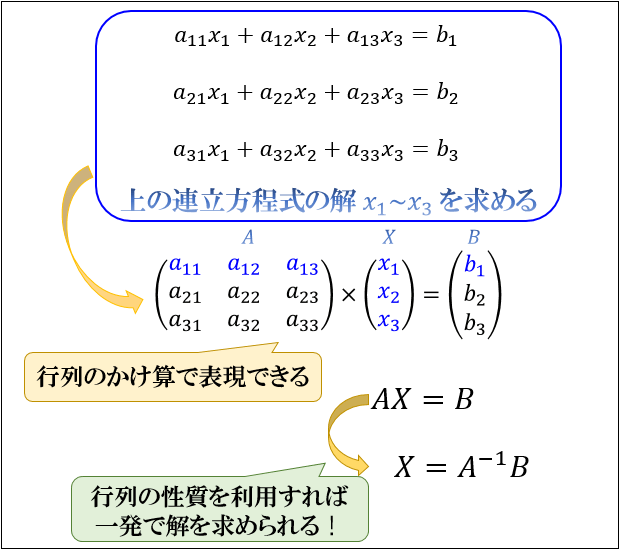
※\(A^{-1}\) :\(A\) の逆行列
これがホントに便利。
コンピューターが発達した現代では、各製品ごとに多くの変数データを扱えるようになりました。
たとえば掃除機であれば「電気代・機動性・吸い込みの強さ・サイズの大きさ・操作のカンタンさ」などなど、たくさんの変数が製品の販売量に影響をあたえています。
そこで、収集されたデータから各製品ごとに「販売量=誤差項+〇×電気代+△×機動性+…」という多元連立方程式をたて、それを最も妥当に説明する回帰式を推定する。
そんなときに行列を使えば、変数が3つ以上の難しい計算もバシッ!と解けるようになるわけです。
日本マクドナルド・ベネッセ・アップルコンピュータ社長を歴任した原田泳幸氏の言葉にもあるように「消費者はどんな商品を求めているか?」は消費者本人に聞いても分かるとは限りません。
例えばお客様に「どんな商品が欲しいですか」とアンケート調査をすると、必ず「低カロリー」とか「オーガニック」とか「ヘルシー」とか、健康重視のメニューが挙がります。
ところが、4枚のパティが入ったメガマックを発売しても、クォーターパウンダーを発売しても、若い女性が平気でメガマックやクォーターパウンダーを食べているわけです。すなわち、お客様のおっしゃることと、実際の行動は全く違うということです。つまりお客様の希望ばかりを聞いて、その通りにしていてはダメなのです。
「消費者は電気代を重視しているように見えたが、意識している以上に機動性や操作のカンタンさを重視しているようだ」といった知見を得るには、大量のデータから分析するほかありません。
行列は、そういった大量のデータをもとにした多次元の連立方程式を1本の式でまとめて考えることを可能にする、非常に便利なツールとなっています。