今回は、「行ベクトルと列ベクトルの内積」・「2×2行列どうしのかけ算」・「l×m行列とm×n行列のかけ算」について書いていきます。
行ベクトルと列ベクトルの内積
行ベクトルと列ベクトルの内積は、以下の式で与えられます。
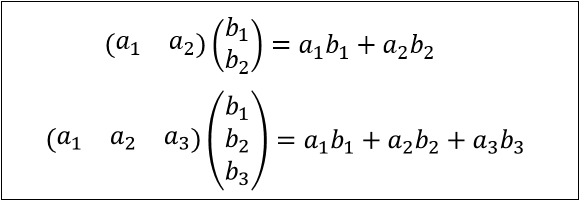
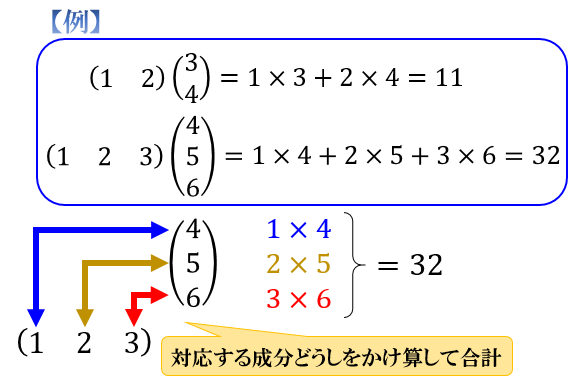
これは、下図のように「対応する成分をかけ算して合計した値」と考えると分かりやすいです。
\(2×2\) 行列どうしのかけ算のやり方
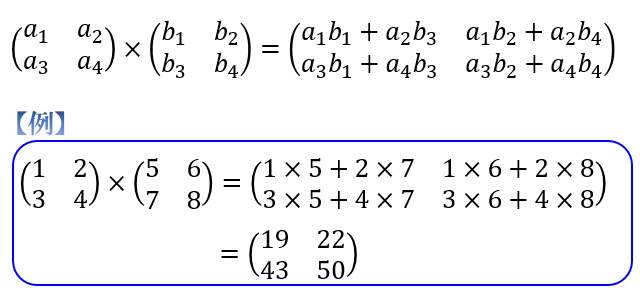
Step① 行・列の平行線と同じ方向に線を引く
まず、「左の行列の行間に横線」「右の行列の列間に縦線」を引きます。
こうすることで、内積を求める行・列の対応が分かりやすくなります。
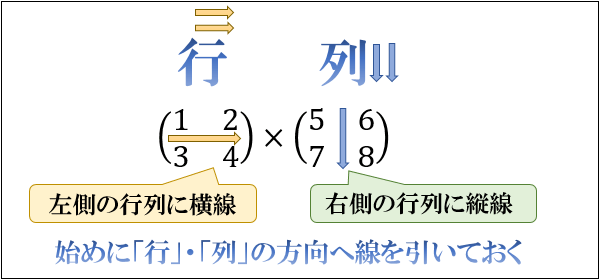
「行」・「列」の漢字右側の平行線と対応させると覚えやすいです。
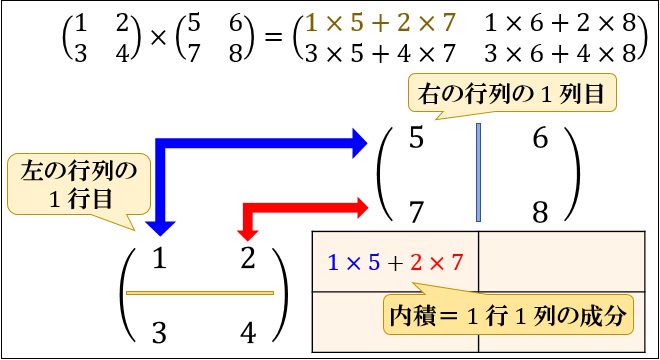
Step② 「左の \(1\) 行目」と「右の \(1\) 列目」の内積=「 \(1\) 行 \(1\) 列の成分」
つぎに、行列の積の1行1列成分を求めます。
1行1列成分は、「左の行列の1行目」と「右の行列の1列目」の内積から求められます。
例題では
左の行列の1行目が \(\left(\begin{array}{cc}1 & 2 \end{array}\right)\)
右の行列の1列目が \(\left(\begin{array}{c}5\\7\end{array}\right)\)
なので、1行1列成分はその内積 \(1×5+2×7=19\) となります。
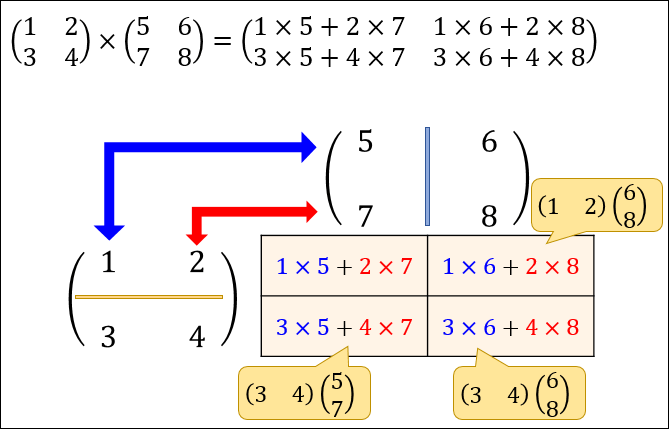
Step③ 「左の \(m\) 行目」と「右の \(n\) 列目」の内積=「\(m\) 行 \(n\) 列の成分」
同じように、他の成分もすべて求めていきます。
\(m\) 行 \(n\) 列成分は、「左の行列の \(m\) 行目」と「右の行列の \(n\) 列目」の内積から求められます。
例題では
左の行列の2行目が \(\left(\begin{array}{cc}3 & 4 \end{array}\right)\)
右の行列の2列目が \(\left(\begin{array}{c}6\\8\end{array}\right)\)
なので、2行2列成分はその内積 \(3×6+4×8=50\) となります。
以上から、2×2行列どうしの積が求まりました。
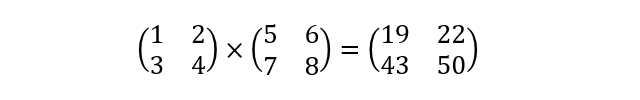
\(l×m\) 行列と \(m×n\) 行列のかけ算の性質
行列どうしのかけ算は、行数・列数が増えても考え方は同じです。
また、行列どうしのかけ算には、以下の性質があります。
① 行列どうしのかけ算は、「左の列数」と「右の行数」が等しくないとかけ算できない
②「\(l\) 行 \(m\) 列の行列」と「\(m\) 行 \(n\) 列の行列」の積が、「\(l\) 行 \(n\) 列の行列」となる