\(n×n\) の行列 \(A\) に対して
\(A \vec{\ x\ }=λ \vec{\ x\ }\)
を満たす「\(\vec{\ 0\ }\) でないベクトル \(\vec{\ x\ }\)」と「スカラー \(λ\) 」の組み合わせが存在するとき、
\(\vec{\ x\ }\) を「\(A\) の固有ベクトル」と言い、\(λ\) を「\(A\) の固有値」と言います。
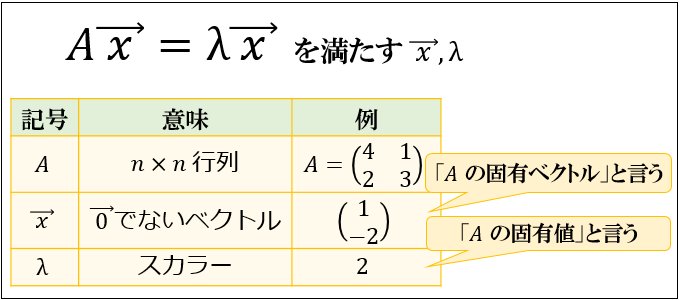
たとえば、\(A=\left(\begin{array}{cc}4 & 1\\2 & 3 \end{array}\right)\) なら
\(\vec{\ x\ }=\left(\begin{array}{c}1\\-2 \end{array}\right)\) かつ \(λ=2\) のときと
\(\vec{\ x\ }=\left(\begin{array}{c}1\\1 \end{array}\right)\) かつ \(λ=5\) のときに
\(A \vec{\ x\ }=λ \vec{\ x\ }\)
が成り立ちます。

参考:行列のかけ算のやり方まとめ。例題から分かる行列の積の考え方
ここから
● \(\left(\begin{array}{c}1\\-2 \end{array}\right)\) と \(\left(\begin{array}{c}1\\1 \end{array}\right)\) (及びその定数倍)は、\(A\) の固有ベクトルである
● \(2\) と \(5\) は、\(A\) の固有値である
と言うことができます。
今回は、この固有ベクトル・固有値の意味と求め方を見ていきましょう。
固有ベクトル・固有値の意味
行列 \(A\) の固有ベクトル \(\vec{\ x\ }\) とは、大雑把に言うと
「行列 \(A\) を掛けても、\(λ\) 倍されるだけで方向が変わらないベクトル」を意味します。
例えば、\(A=\left(\begin{array}{cc}\dfrac{3}{2} & 2\\1 & \dfrac{1}{2} \end{array}\right)\) を色んなベクトルに掛けると、ベクトルはどう変化するでしょうか?
実際に、行列のかけ算を行ってみると
\(\left(\begin{array}{c}0\\1 \end{array}\right)\) に \(A\) を掛けると \(\left(\begin{array}{c}2\\\dfrac{1}{2} \end{array}\right)\) に
\(\left(\begin{array}{c}-1\\0 \end{array}\right)\) に \(A\) を掛けると \(\left(\begin{array}{c}\dfrac{-3}{2}\\-1 \end{array}\right)\) に変換されることが分かります。
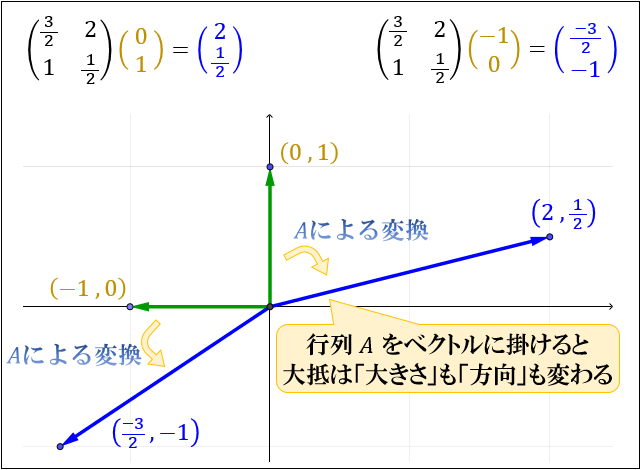
このように、行列 \(A\) を掛けると「ベクトルの大きさ」も「ベクトルの方向」も変化するのが普通です。
しかし、中には \(A\) を掛けても「方向」が変わらないベクトルもあります。
たとえば、\(\left(\begin{array}{c}1\\ \dfrac{1}{2} \end{array}\right)\) や \(\left(\begin{array}{c}1\\-1 \end{array}\right)\) は \(A\) を掛けても、それぞれ \(\dfrac{5}{2}\) 倍, \(-\dfrac{1}{2}\) 倍されるだけでベクトルの方向は変わっていません。(180°反転はマイナス倍された同じ方向)

このように、行列 \(A\) を掛けても定数 \(λ\) 倍されるだけで方向は変わらないベクトル。
それが、\(A\) の固有ベクトルです。
このときの定数 \(λ\) を「\(A\) の固有値」と言います。
固有方程式
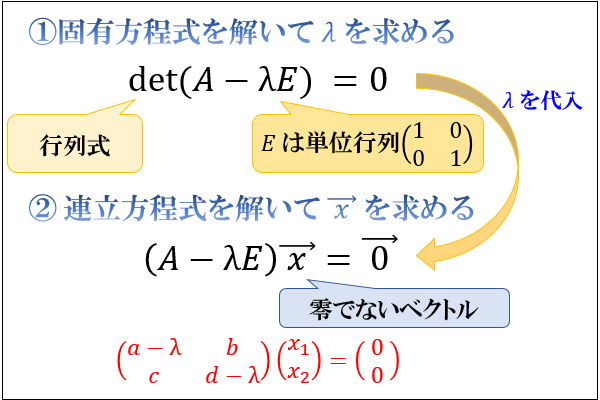
行列 \(A\) の固有ベクトル \(\vec{\ x\ }\) と固有値 \(λ\) は、固有方程式 \(\det(A-λE)=0\) を \(λ\) の方程式として解くことで求まります。
【例題】\(A=\left(\begin{array}{cc}\dfrac{3}{2} & 2\\1 & \dfrac{1}{2} \end{array}\right)\) の固有ベクトル・固有値を求めてください。
まず、固有方程式を解いて \(A\) の固有値を求めます。

固有方程式を解くことで、\(A\) の固有値 \(λ=\dfrac{5}{2},\dfrac{-1}{2}\) が求まりました。
固有値が求まったら、次はそれらに対応する固有ベクトルを求めます。
まずは、\(λ=\dfrac{5}{2}\) に対応する固有ベクトル。

\(x_1=2x_2\) を満たすことが固有ベクトルとなる条件だと分かるので
\(\left(\begin{array}{c}1\\ \dfrac{1}{2} \end{array}\right)\) と、その定数倍すべてが \(A\) の固有ベクトルだと分かります。
次は、\(λ=\dfrac{-1}{2}\) に対応する固有ベクトル。

\(x_1=-x_2\) を満たすことが固有ベクトルとなる条件だと分かるので
\(\left(\begin{array}{c}1\\ -1 \end{array}\right)\) と、その定数倍すべてが \(A\) の固有ベクトルだと分かります。
● \(A=\left(\begin{array}{cc}\dfrac{3}{2} & 2\\1 & \dfrac{1}{2} \end{array}\right)\) の固有ベクトルは \(\left(\begin{array}{c}1\\ \dfrac{1}{2} \end{array}\right)t\) , \(\left(\begin{array}{c} 1\\-1 \end{array}\right)t\) ( \(t\) は \(t≠0\)の任意の定数)である
● \(A\) の固有値は \(\dfrac{5}{2}\) と \(\dfrac{-1}{2}\) である
固有ベクトル・固有値を理解するとできること
固有ベクトル・固有値は、統計学においては主成分分析という形で利用されています。
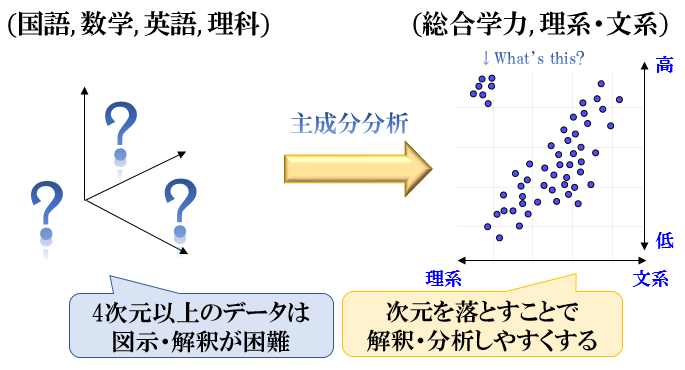
主成分分析とは「変数が3つ以上ある高次元のデータに対して、より低い次元でデータのばらつきを説明する」手法です。
たとえば、生徒の成績が「国語 \(x_1\)」「数学 \(x_2\)」「英語 \(x_3\)」「理科 \(x_4\)」の4次元データで表わされる場合。
ぼくたちヒトは、平面で図示できる2次元データを解釈するのは得意ですが、4次元以上のデータを図示・解釈するのは得意ではありません。
そのため、4次元データのままだと生徒の成績の分析をするのが難しいという問題があります。
そこで役に立つのが、主成分分析。
生徒の成績を主成分分析によって「総合学力指標 \(z_1\)」「理系・文系指標 \(z_2\)」という2次元平面に落とし込むことにより、各生徒の特徴付けや分類をしやすくなり、分析の質を高めることができるのです。
皆さんも学生のころ、友人の成績1つ1つをすべて把握するのは難しくても「A君は総合学力が非常に高く文系科目に強い」「B君は総合学力がそこそこ高く理系科目に強い」といったような次元を落とした把握なら自然とできていたのではないでしょうか。
あれを数理的に行うのが主成分分析であり、その計算に必要なツールこそが固有ベクトルと固有値なのです。
ぜひ、活用してください。