
このページでは、「\(2×2\) 行列の逆行列の求め方」と「\(3×3\) 行列の逆行列の求め方」を具体例を通じてみていきます。
\(2×2\) 行列の逆行列の求め方
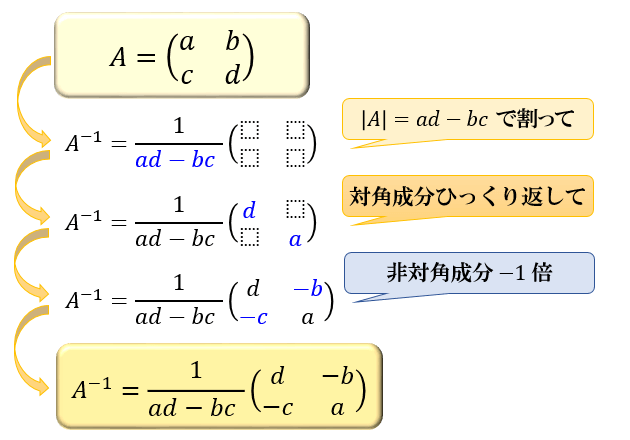
\(A=\left(\begin{array}{cc}a & b\\c & d \end{array}\right)\) の逆行列 \(A^{-1}\) は、以下の公式で表されます。
\(A^{-1}=\dfrac{1}{ad-bc}\left(\begin{array}{cc}d & -b\\-c & a \end{array}\right)\)
公式だけ見ると少しややこしそうに見えるかもしれませんが、以下の3つのステップで計算するとラクに求められます。
Step①:行列式 \(|A|=ad-bc\) で割る
Step②:対角成分をひっくり返す
Step③:非対角成分を \(-1\) 倍する
問1: \(B=\left(\begin{array}{cc}1 & 2\\ 3 & 4 \end{array}\right)\) のとき、\(B^{-1}=\ ?\)

問2: \(C=\left(\begin{array}{cc}8 & -3\\ -4 & 2 \end{array}\right)\) のとき、\(C^{-1}=\ ?\)

3つのステップを通じて計算してみると、意外とカンタンに求められるのが分かりますね。
逆行列 \(A^{-1}\) を正しく求められたかチェックしたいときは、元の行列 \(A\) とかけ算してみてください。
かけ算した結果が単位行列 \(\left(\begin{array}{cc}1 & 0\\0 & 1 \end{array}\right)\) になれば、正しく逆行列を求められたことが分かります。

\(3×3\) 行列の逆行列の求め方
\(3×3\) 行列や \(4×4\) 行列などの逆行列は、「掃き出し法」を使って求めるとラクです。
掃き出し法とは、「\(n×n\) 行列 \(A\)」と「\(n×n\) の単位行列 \(E\)」があったとき
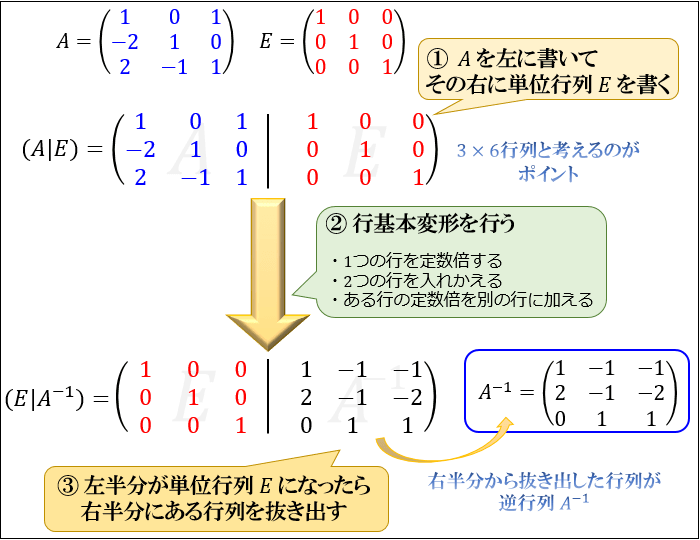
Step①:\(A\) と \(E\) を合体させた行列 \((A|E)\) を書く
Step②:\((A|E)\) に行基本変形を行って、行列左半分の対角成分を \(1\) ・非対角成分を \(0\) にする
Step③:行列の左半分が単位行列 \(E\) になったとき、右半分の行列を抜き出すと \(A^{-1}\) が求まる
という3つのステップから逆行列 \(A^{-1}\) を求める手法です。
問3: \(A=\left(\begin{array}{ccc}1 & 3 & 2\\ -1 & 0 & 1\\2 & 3 & 0 \end{array}\right)\) のとき、\(A^{-1}=\ ?\)
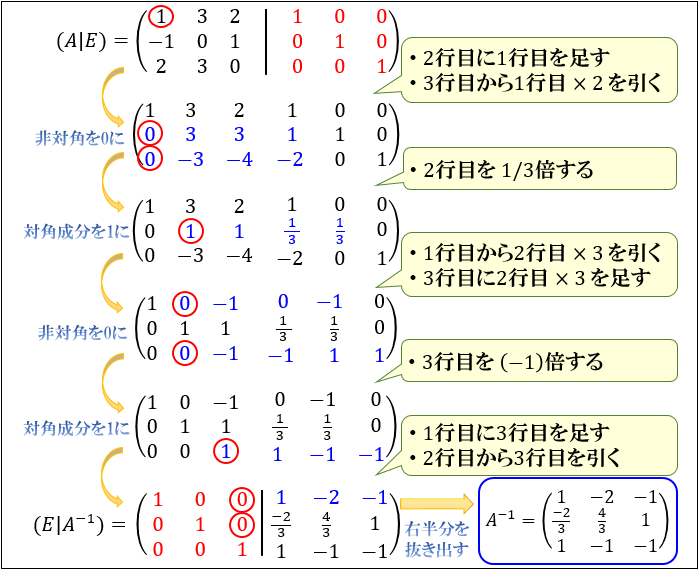
上図の赤丸の順に、非対角成分を \(0\) ・対角成分を \(1\) に変形していくのがポイントです。
以上から
\(A^{-1}=\left(\begin{array}{ccc}1 & -2 & -1\\ -\dfrac{2}{3} & \dfrac{4}{3} & 1\\1 & -1 & -1 \end{array}\right)\)
と求まりました。
実際に、元の行列 \(A\) とかけ算すると単位行列 \(E\) になることから、正しく逆行列を求められたことが分かります。





