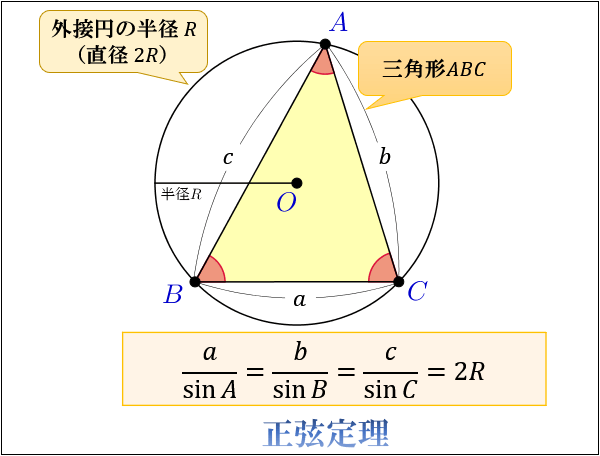
三角形 \(ABC\) に対して、点 \(A,B,C\) の内角をそれぞれ角 \(A,B,C\) とおき
点 \(A\) の反対側にある線分 \(BC\) の長さを \(a\)
点 \(B\) の反対側にある線分 \(CA\) の長さを \(b\)
点 \(C\) の反対側にある線分 \(AB\) の長さを \(c\)
三角形 \(ABC\) に外接する円の半径を \(R\)
とおいたとき、以下の等式が成り立つことを正弦定理と言います。
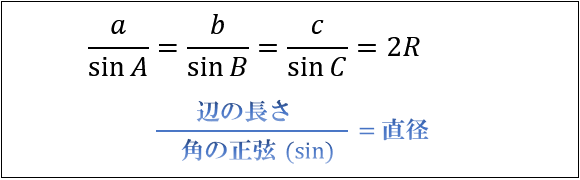
三角形の向い合う辺と角に対して
「辺の長さ」と「角の正弦(sin)」の比は常に外接円の直径 \((2R)\) と等しくなる。
それが、正弦定理です。
垂直な補助線から分かる正弦定理
向かい合う辺と角について「辺の長さ」と「角の正弦(sin)」の比が一定であることは、下図のように直線 \(BC\) と垂直に交わる補助線 \(AD\) を引くと分かりやすくなります。
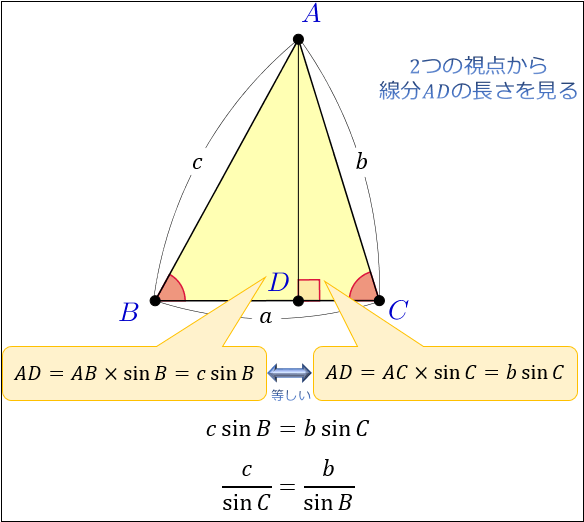
まずは、左側の直角三角形 \(ABD\) に注目してみてください。
\(ABD\) の斜辺の長さは \(AB=c\) なので、三角関数の定義から \(AD= c\ \sin{B}\) と分かりますね。
次に、右側の直角三角形 \(ACD\) に注目。
直角三角形 \(ABD\) の斜辺の長さは \(AC=b\) なので、同様に \(AD= b\ \sin{C}\) と求まります。
これらは同じ線分 \(AD\) に関する等式なので、\(c\ \sin{B}=AD=b\ \sin{C}\) となり
両辺を \(\sin{B}×\sin{C}\) で割ると \(\dfrac{c}{\sin{C}}=\dfrac{b}{\sin{B}}\) が求まり、正弦定理の形になりました。
\(\dfrac{c}{\sin{C}}=\dfrac{b}{\sin{B}}\) が求まったら、次は \(\dfrac{c}{\sin{C}}=\dfrac{a}{\sin{A}}\) を求めましょう。
これは、さきほどと同じ流れを直線 \(AC\) と垂直に交わる補助線 \(BE\) について考えればOKです。
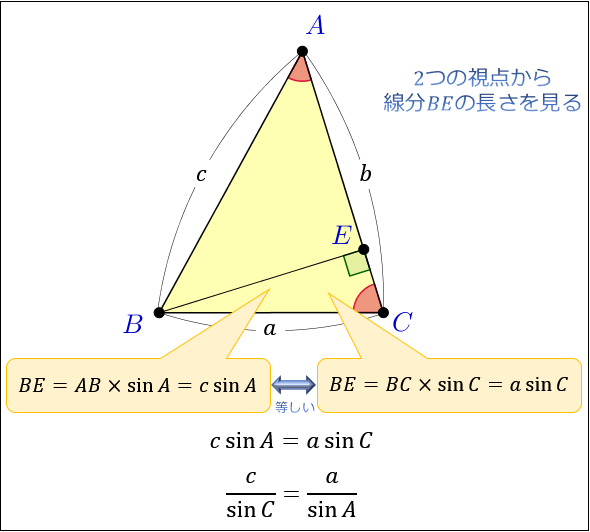
ここから、\(\dfrac{c}{\sin{C}}=\dfrac{a}{\sin{A}}\) が成立。
結果、\(\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}\) となって
向かい合う辺と角について「辺の長さ」と「角の正弦(sin)」の比が一定であることを示せました。
円周角の定理
「辺の長さ」と「角の正弦(sin)」の比が外接円の直径 \((2R)\) と等しくなることは、円周角の定理を利用すると分かりやすくなります。
円周角の定理とは「1つの弧 \(BC\) に対する中心角 \(∠BOC\) は円周角 \(∠BAC\) の \(2\) 倍の大きさになる」という定理です。
\(∠BOC=2×∠BAC\)
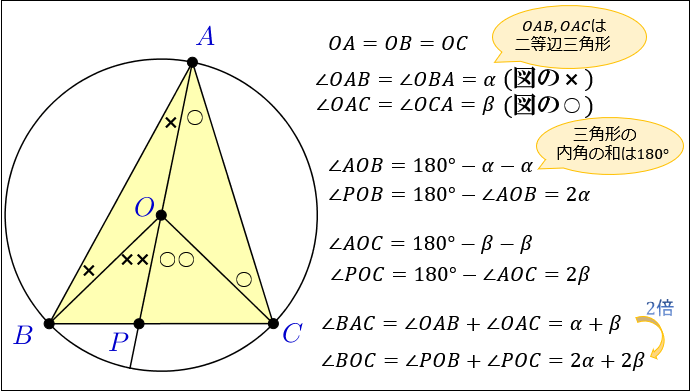
円周角の定理は、上図のように「二等辺三角形の底角が等しいこと」「三角形の内角の和は \(180°\) であること」を利用することで証明できます。
円周角の定理から分かる正弦定理
円周角の定理から \(∠BOC=2×∠BAC\) が分かったら、次は線分 \(BC\) の中点 \(M\) を考えます。
\(M\) は線分 \(BC(=a)\) の中点なので、\(BM\) の長さは \(\dfrac{a}{2}\)
三角形 \(OBM\) と \(OCM\) は合同より、\(∠OMB=90°\)
\(∠BOM\) は「\(∠BOC\) の半分」なので、\(∠BOM=(2×∠BAC)÷2\) となり、\(∠BOM\)と \(∠BAC\) が等しくなることが分かります。
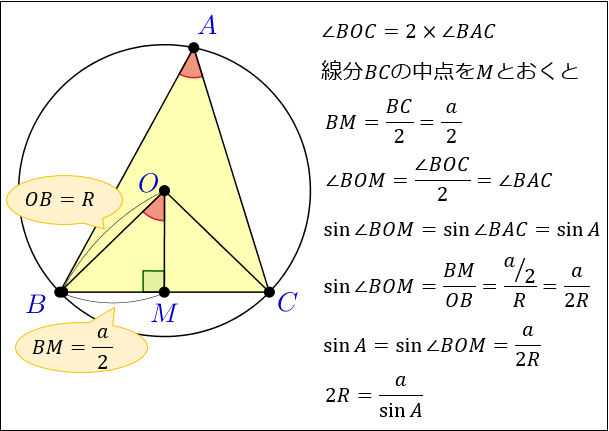
あとは、直角三角形 \(OBM\) に注目すると
\(\sin{∠BOM}=\dfrac{BM}{OB}=\dfrac{a}{2R}\)
\(\sin{∠BOM}=\sin{A}\) から、\(\sin{A}=\dfrac{a}{2R}\) ⇔ \(2R=\dfrac{a}{\sin{A}}\) を導くことができました。
余弦定理と比べると使用頻度が低いせいか、意外とド忘れしやすい定理だと思います。図を使って形を覚えておくと忘れにくいですね。