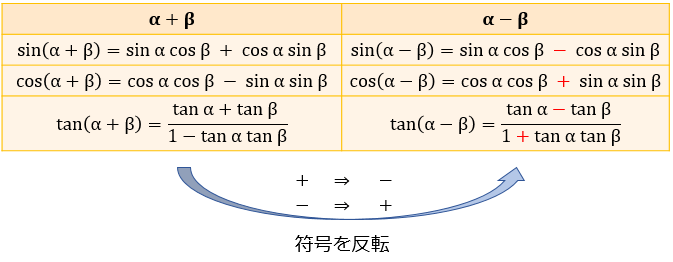
加法定理とは、「\((α ± β)\) に対する三角関数」を「 \(α\) や \(β\) に対する三角関数」で表す公式のこと。
この加法定理の中でも特に重要なのが以下の2つです。
\(\sin{(α+β)}=\sin{α}\cos{β}+\cos{α}\sin{β}\)
\(\cos{(α+β)}=\cos{α}\cos{β}-\sin{α}\sin{β}\)
この2つの公式さえ暗記できれば、残りの公式は簡単に求められるようになります。
\(\tan{(α+β)}\) の公式 ⇒ \(\dfrac{\sin{(α+β)}}{\cos{(α+β)}}\) の分母分子を \(\cos{α}\cos{β}\) で割る
\((α-β)\) の公式 ⇒ \((α+β)\) の公式の中の「+と-」を反転させる
今回は、加法定理の公式の考え方を図形を通じて解説していこうと思います。
加法定理の考え方の流れ
加法定理は、3つの直角三角形をくっつけた台形 \(ABED\) を考えると分かりやすくなります。
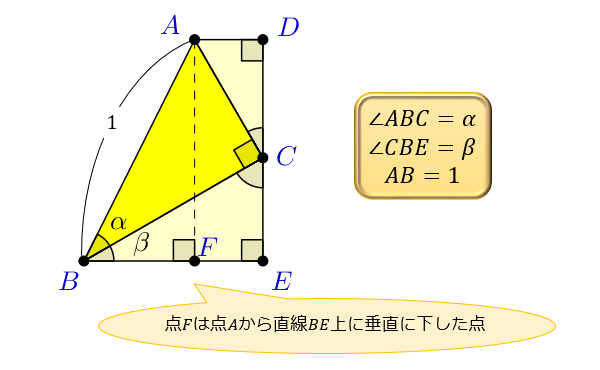
\(∠ABC=α,∠CBE=β,AB=1\) とおいて、考えていきましょう。
Step①三角形ABC
まずは、この図形の真ん中にある三角形 \(ABC\) に注目してみましょう。
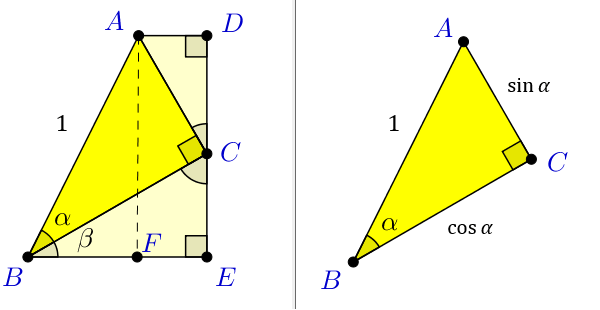
この三角形 \(ABC\) は「斜辺の長さ \(1\) ,\(∠ABC=α\) の直角三角形」です。
そのため、三角比の定義から \(AC=1×\sin{α} , BC=1×\cos{α}\) であることが分かります。
\(AC=\sin{α}\)
\(BC=\cos{α}\)
Step②三角形ACDと三角形CBE
\(AC\) と \(BC\) が求まったら、今度は三角形 \(ACD\) と三角形 \(CBE\) に注目してみましょう。
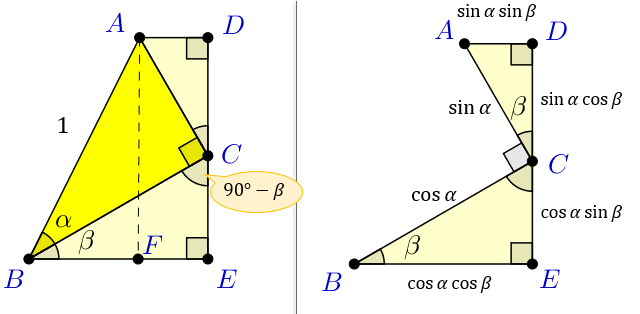
ここでは、\(∠ACD=∠CBE=β\) となるのがポイントです。
※ \(∠ACD=β\) の求め方
\(DCE\) は直線なので \(∠DCE=180°\)
つまり \(∠ACD+∠ACB+∠BCE=180°\)
\(∠ACB\) は直角なので \(∠ACB=90°\)
\(∠BCE\) は三角形の内角の和は \(180°\) より
\(∠BCE=180°-∠CBE-∠CEB\) \(=180°-β-90°=90°-β\)
よって \(∠ACD=180°-∠ACB-∠BCE\) \(=180°-90°-(90°-β)=β\)
この2つの三角形に注目すると
三角形 \(ACD\) は「斜辺の長さ \(\sin{α}\) ,\(∠ACD=β\) の直角三角形」なので
\(AD=\sin{α}×\sin{β},CD=\sin{α}×\cos{β}\)
三角形 \(CBE\) は「斜辺の長さ \(cos{α}\) ,\(∠CBE=β\) の直角三角形」なので
\(CE=\cos{α}×\sin{β} ,BE=\cos{α}×\cos{β}\)
であることが分かりますね。
\(AD=\sin{α}×\sin{β}\)
\(CD=\sin{α}×\cos{β}\)
\(CE=\cos{α}×\sin{β}\)
\(BE=\cos{α}×\cos{β}\)
Step③長方形ADEF
\(AD,CD,CE,BE\) が求まったら、次は三角形 \(ABF\) と長方形 \(ADEF\) に注目。
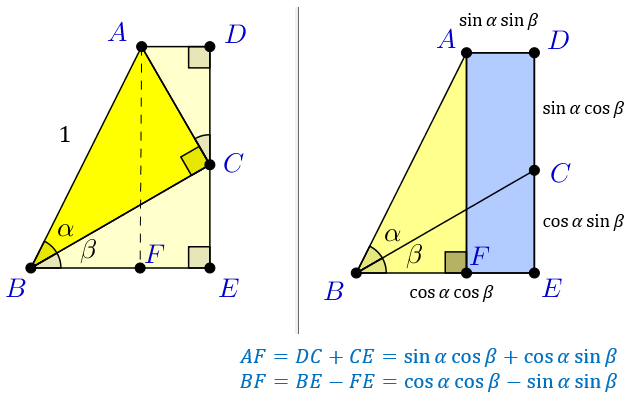
まず長方形 \(ADEF\) に注目すると、この長方形は
横の長さが \(FE=AD=\sin{α}\sin{β}\)
縦の長さが \(AF=DE=DC+CE\) \(=\sin{α}\cos{β}+\cos{α}\sin{β}\)
であることが分かります。
次に三角形 \(ABF\) に注目すると、この三角形は
高さが \(AF=\sin{α}\cos{β}+\cos{α}\sin{β}\)
底辺が \(BF=BE-FE=\cos{α}\cos{β}-\sin{α}\sin{β}\)
の直角三角形であることが分かりますね。
ここまで来ればあと少しです。
\(AF=\sin{α}\cos{β}+\cos{α}\sin{β}\)
\(BF=\cos{α}\cos{β}-\sin{α}\sin{β}\)
Step④三角形ABF
\(BF\) と \(AF\) の長さが求まったら、いよいよ大詰めです。
三角形 \(ABF\) が「斜辺の長さ \(1\) ,\(∠ABF=(α+β)\) の直角三角形」であることに注目すると
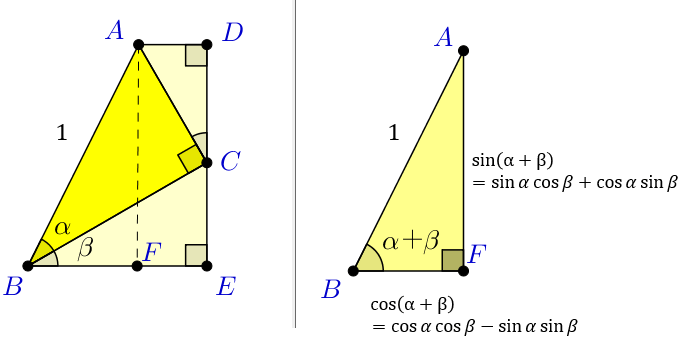
三角比の定義から
\(AF=1 × \sin{(α+β)}\)
\(BF=1 × \cos{(α+β)}\)
であることが判明。
ここに、先ほど求まった \(AF=\sin{α}\cos{β}+\cos{α}\sin{β}\) と \(BF=\cos{α}\cos{β}-\sin{α}\sin{β}\) を代入すると
\(\sin{(α+β)}=\sin{α}\cos{β}+\cos{α}\sin{β}\)
\(\cos{(α+β)}=\cos{α}\cos{β}-\sin{α}\sin{β}\)
みごと、加法定理を示すことができました。