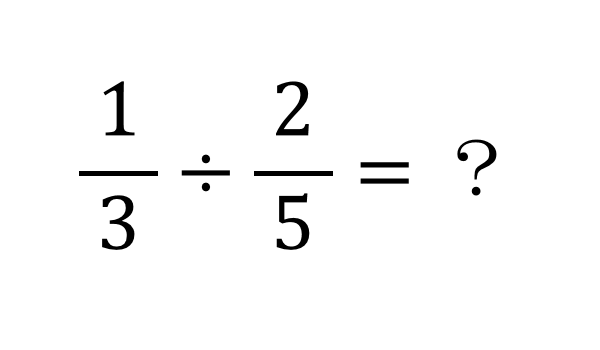
\(y=f(x)\) を \(x\) で微分したいとき、対数を取ってから微分した方が楽なケースがあります。
このような「両辺の対数を取ってから微分する」手法。それが、対数微分法です。
対数微分法の手順
手順にしたがって、対数微分法のやり方を見ていきましょう。
step①両辺の絶対値の自然対数をとる
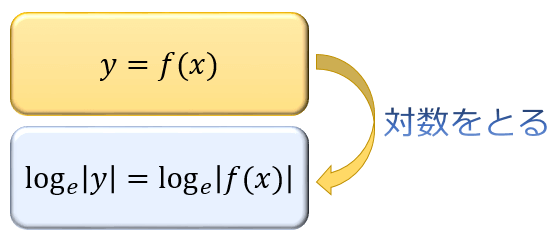
まず、\(y=f(x)\) の両辺の絶対値の対数を取ります。
ここでは、微分と相性が良いネイピア数 \(e\) を底とする自然対数 \(\log_{e}|y|\) を使うのがポイント。
こうすることで、次に行う微分が楽になります。
なぜ絶対値の対数 \(\log_{e}|y|\) を使うのかというと、「\(e\) は何乗しても負の値にはならない」ので、対数 \(\log_{e}M\) は真数条件 \(M>0\) を満たさなければならないからです。
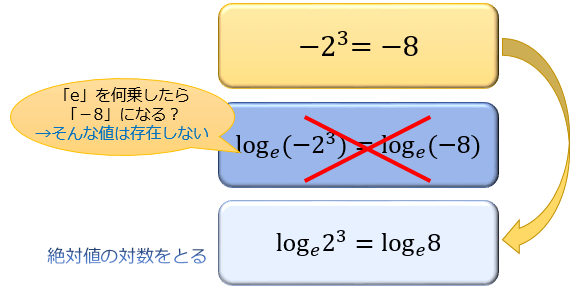
両辺が正の値であることが明らかであれば、絶対値を使わない \(\log_{e}y\) でOKです。
step②両辺を \(x\) で微分する
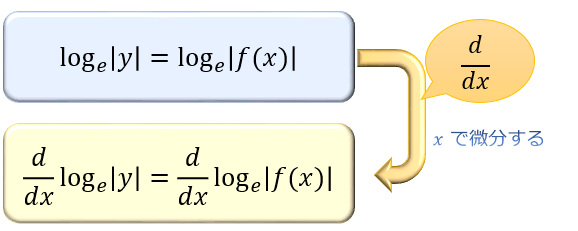
次に、両辺を \(x\) で微分します。
対数には、真数のかけ算が対数の足し算、真数の累乗が対数のかけ算になる性質があります。
そのため、そのままだと微分しにくかった \(f(x)\) でも、対数の性質を利用することで微分しやすい形になるというわけです。
step③合成関数の微分公式を使う

次に、合成関数の微分公式を使います。
式だけを見るとややこしそうですが、「\(x\) では直接微分できないので、まず \(y\) で微分した後に、\(y\) を \(x\) で微分した値 \(dy/dx\) をかけることで帳尻を合わせている」と考えると式の意味がイメージしやすいです。
この合成関数の微分公式を使うと…
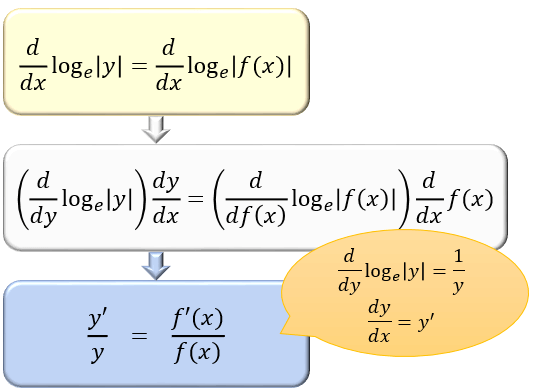
左辺が \(y’/y\) になることが分かります。
step④両辺に \(y\) をかける
最後に、両辺に \(y\ (=f(x))\) をかけてやれば…
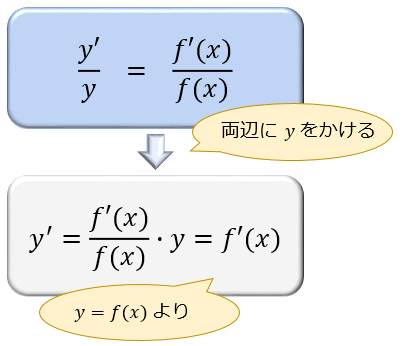
みごと、\(y=f(x)\) を \(x\) で微分した値 \(y’\) が求まりました。これが、対数微分法です。
パッと見は回り道をしているように感じるかもしれませんが、複雑な関数だとこの手法がすごく便利です。具体的に計算してみた方が理解も早いので、いくつか具体例を見ていきましょう。
具体的な計算方法
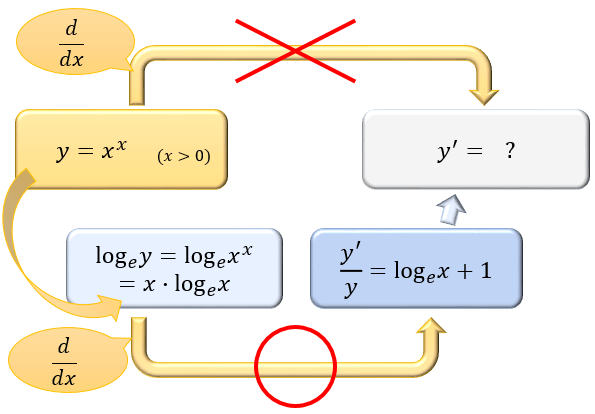
まずは \(y=x^x\ (x>0)\) の微分。
そのままだと、どう微分したら良いか分かりませんよね。
こんな関数でも、対数微分法なら簡単に微分することができるんです。
今回は、両辺とも正の値なので step① で絶対値を使う必要はありません。

※ \((\log_{e}x)’=1/x\) を使っています。これの証明は以下の記事を参考に。
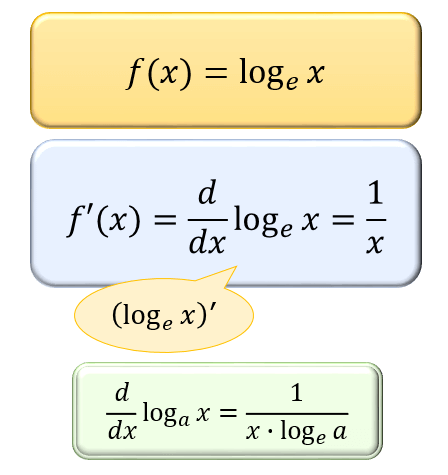
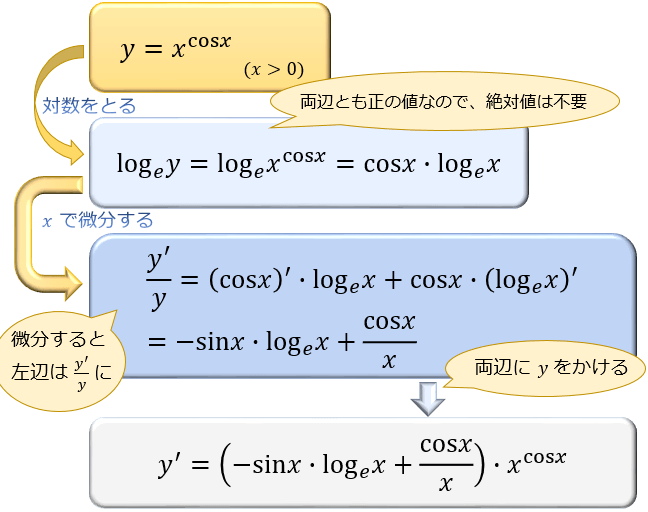
次は、\(y=x^{cosx}\ (x>0)\) の微分。
ぼくも、初めて対数微分法を勉強した時は「これが何の役に立つんだろう…」なんて思っていましたが、大学生になってからデータ分析や機械学習を勉強し始めたら当たり前のように沢山出てきてビックリした思い出があります。
経済学でも対数変換してから微分する考え方がよく出てくるので、対数や合成関数の微分はぜひおさえておきたいところ。