
数学の中でも暗記が通用しにくく、論理的思考力が求められる「確率」。
確率とは「ある事柄が現れる割合・発生の度合い」を表わす数値のこと。
これを知ることで色んな局面でより有利な選択ができるようになる、実用性の高い数値です。
今回はそんな確率計算の公式と、つまずきやすいポイントの対策について書いていきます。
photo credit:: Brett Taylor
中学数学における確率計算の公式
中学数学の確率の問題では、この公式が便利です。
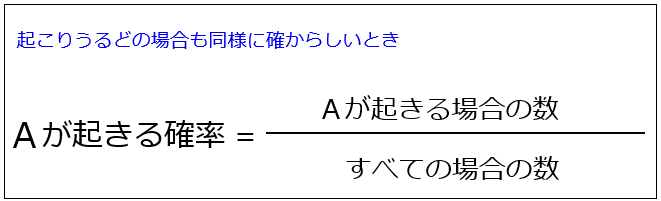
※「場合の数」とは、何通りあるかを表わす数。「パターン数」と言いかえると分かりやすい
例)サイコロを1回振って「2」が出る確率は?
例えば、サイコロを1回振って「2」が出る確率を求める問題では、公式をこう使います。
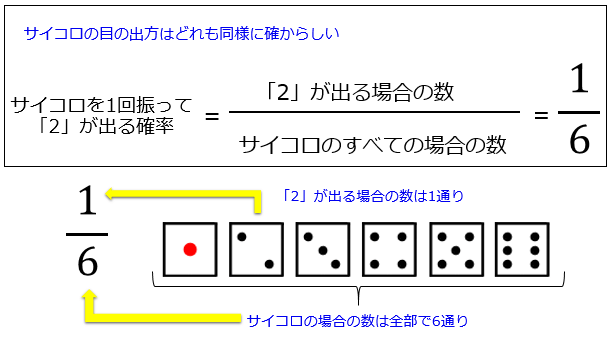
サイコロを1回振って「2」が出る確率は
「2」が出る場合の数が1通り、すべての場合の数が6通りなので「1通り/6通り」で 1/6 となります。
似ているようで、まったく違う2つの確率計算問題
このように、シンプルな確率の問題では確率を求めたい事柄の「場合の数」を分子にし、すべての「場合の数」を分母にすることで楽に答えを出すことができます。
しかし、問題のレベルが上がるにつれ、「場合の数」だけで考えていると間違えやすい問題も出てくるようになります。
これは「似ているようで、まったく違う2種類の確率計算問題が存在する」のが原因です。
この2種類の問題の違いさえ理解すれば、確率問題の正解率がグッと上がってきます。
つぎの問題①と問題②を注意して読み比べて、その違いを考えてみましょう。
問題①帰る経路をランダムに決めるパターン
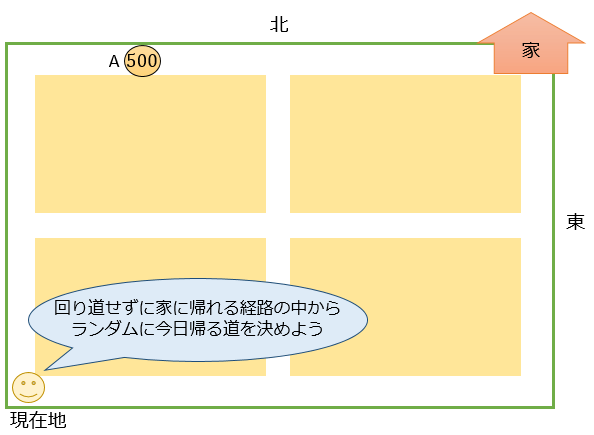
田んぼの「田」のような道路(下図参照)があるとする。
今、左下の「現在地」から右上の「家」へ最短距離で帰る経路をランダムに決める。
経路は北と東にのみ進むものの中から選ばれ、各経路が選ばれる確率は全て同じとする。
このとき、500円玉が落ちているA地点を通る確率を求めて下さい。
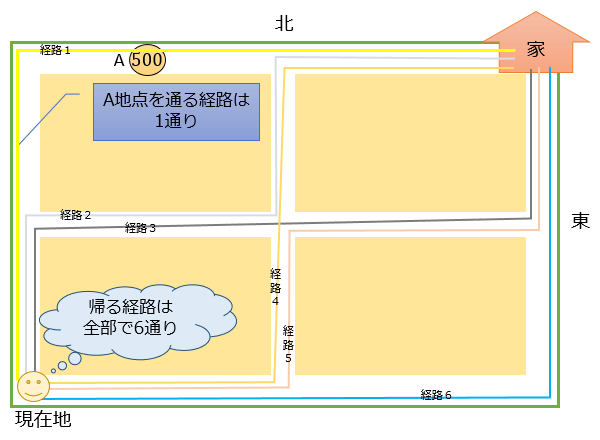
この問題は、先ほどの公式をそのまま当てはめるだけで解くことができます。
この道路を回り道せずに帰る経路はぜんぶで6通り、そのうちA地点を通るのは1通り。
よって、答えは「1通り/6通り」で1/6となります。
問題②北に進むか東に進むかをコインで決めるパターン
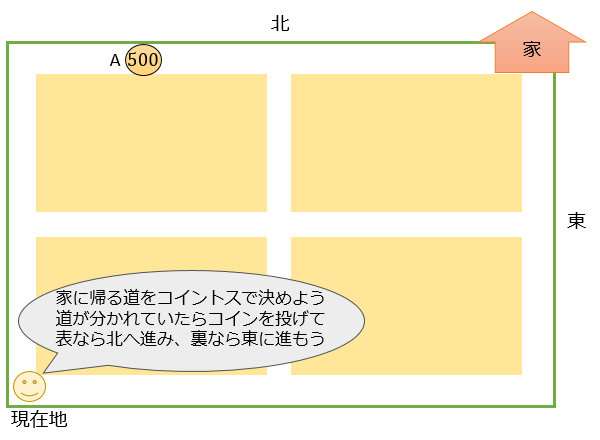
田んぼの「田」のような道路(下図参照)があるとする。
今、左下の「現在地」から右上の「家」へ最短距離で帰る経路をコイントスで決める。
道が分かれていたらコインを投げ、表が出れば北へ・裏が出れば東へ進む。
コインを投げて表が出る確率と裏が出る確率は同じとする。
このとき、500円玉が落ちているA地点を通る確率を求めて下さい。
パッと見は「さっきと同じ問題じゃないの?」と思うかもしれませんが、実は全く違う問題なんです。
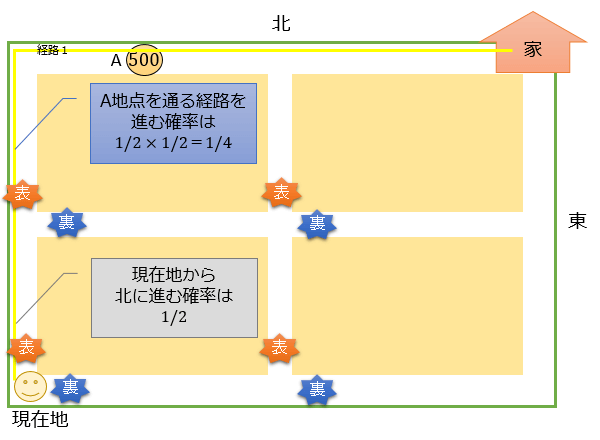
この問題の場合は、まず現在地で表を出して北に進み、次の分かれ道でも表を出せばA地点を通れますよね?
つまり、2回連続で表を出せばA地点を通ることになります。
コインの出方は表と裏の2通りで、表が出るのは1通り。
そのため、コインを投げて表が出る確率は1/2です。
そして今回は「A地点を通る=2回連続で表が出る」確率を求めたいので
答えは1/2×1/2=1/4となります。
よく似た問題なのに「問題①は1/6。問題②は1/4」と異なる答えが出てきました。
なぜ答えが変わって来るのか、じっくりと考えてみましょう。
「同様に確からしい」事柄が違う
なぜ、似たような問題なのにこのような差が出てくるのか。
その答えは、先ほどいったん無視していた「同様に確からしい」にあります。
「同様に確からしい」とは、簡単に言うと「同じ確率である」と考えられるもののこと。
この「同様に確からしい」という視点から2つの問題を見比べてみてください。
問題①で「同様に確からしい」のは「各経路が選ばれる確率」
問題②で「同様に確からしい」のは「コインの表が出る確率と、裏が出る確率」
この2つの問題は、「同様に確からしい」事柄が違いますよね?
そのため、公式を当てはめる場所が変わってくるんです。

これにより
問題①では「経路の場合の数」に公式を当てはめて「1通り/6通り=1/6」
問題②では「コインの場合の数」に公式を当てはめて「1通り/2通り × 1通り/2通り=1/4」
と異なる答えが出てきた、ということなんです。
確率問題でよくあるミスが「同様に確からしい『場合の数』を勘違いすること」です。
確率の問題では「どの場合の数が同様に確からしいのか?」に注目して問題文を読み、同様に確からしい「場合の数」に公式を当てはめるクセをつけると、正解率がグッと上がってきますよ。
同様に確からしい場合の数に注目するクセをつけると、ゲームで有利に動けるようになる
①確率の計算問題では「起こりうるどの場合も同様に確からしいとき、Aが起きる確率=Aが起きる場合の数/すべての場合の数」という公式が便利。
②一見すると似たような問題でも、「同様に確からしい」事柄が違うだけで、まったく違う答えが出てくるようになる。
③確率の問題で間違える主な原因は、同様に確からしい「場合の数」を勘違いすること。
④確率の問題を解くときは、すぐに場合の数を調べるのではなく、「どの場合の数が同様に確からしいのか?」に注目して問題文を読み、同様に確からしい場合の数に公式を当てはめるクセをつけると正解しやすくなる。
一見すると面倒くさそうな「同様に確からしい」ですが、これを理解するとマーケティングや投資・財務分析で非常に役に立ってくる武器になってきます。
 By: motoyen
By: motoyen
身近な例だと、ゲームで自分に有利な選択を考えるうえでも強力な武器となってくれますよ。
例えば・・・
①すごろくで3マス先の「ふりだしに戻る」を避けたい
→サイコロを1つ投げた時は「3」と「4」の確率は同様に確からしいが、サイコロを2つ投げた時の合計では同様に確からしくなく、「4」の確率の方が高い
→ここでサイコロを2つ投げられるカードを使おう!
②「コインを5回投げて表が出た回数+1」か「サイコロを振って出た目」のどちらかを選んで、相手より大きな数を出せば勝ち(同数なら引き分け)
→同様に確からしい事柄が違うので、数の出方に差がある
→相手が「3以下」を出したときはコインをえらんだ方が良いし、相手が「4以上」を出したときはサイコロをえらんだ方が良い。(確率変数の記事を参考)
一度理解しておけば、いろんな場面ですぐに使えて一生重宝する考え方なので、ぜひ色んな確率問題にトライして「同様に確からしい『場合の数』はどれか?」を探す思考法をマスターしてください!





