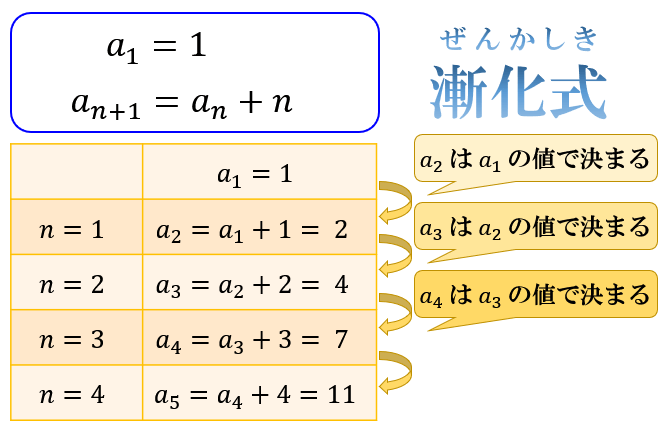
置換積分法とは、変数をうまく変換することで計算量を減らすテクニックです。
たとえば、$\displaystyle \int x(2-x)^4 dx$ を考えてみましょう。
この積分は、このままだと \((2-x)^4\) を展開しないと積分の公式を当てはめることができません。
しかし、\((2-x)^4\) の展開はかなり手間がかかりますし、力技で解けても応用が効きません。

そこで \((2-x)=t\) と変換することで積分の公式を使いやすい形に変え、計算を楽にする。
それが、置換積分法です。
今回は、置換積分のやり方とコツを5つのステップに分けて解説していきます。
置換積分のやり方とコツ
置換積分法は、大きく分けて5つのステップから成り立っています。
以下の例題を通じて、順にみていきましょう。
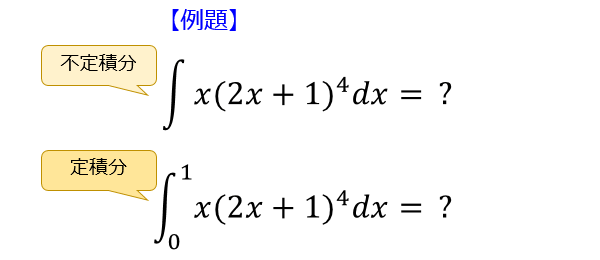
Step① \(=t\) に置きかえるものを決める
まず、\(x\) を使った式を \(t\) に置きかえます。
例題では、\((2x+1)^4\) の展開をする手間をなくしたいので、\(2x+1=t\) と置きます。

「どの部分を \(t\) に置きかえるか」の判断には慣れが必要ですが、
とりあえずはルートや累乗のなかの複雑なかたまりを \(t\) と置いてみるとうまく行くことが多いです。

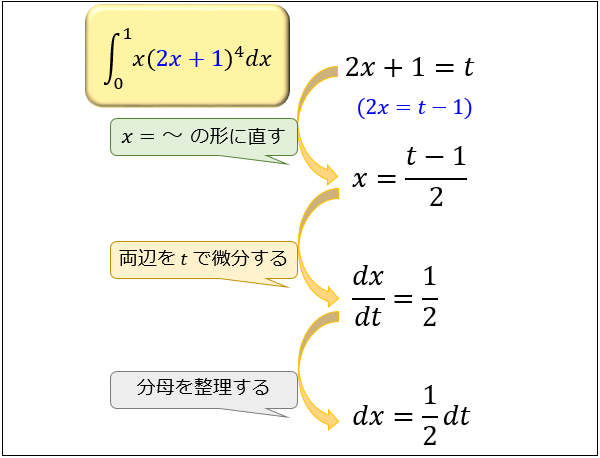
Step② \(x=g(t)\) の形に変換して \(t\) で微分。\(dx/dt\) を求める
次に、Step①で置いた「 \(x\) と \(t\) の式」を
\(x=g(t)\) の形に直してから \(t\) で微分して \(dx/dt\) を求めます。
例題では、\(2x+1=t\) を式変形して \(x=\dfrac{t-1}{2}\)
これを \(t\) で微分して \(dx/dt=\dfrac{1}{2}\) となります。
\(dx/dt\) が求まったら、分母を整理して \(dx=\dfrac{1}{2} dt\) の形にしておくのがオススメです。
Step③ 定積分なら積分区間 \(a→b\) も置きかえる
不定積分では、このステップは飛ばしてOKです。
定積分では、積分区間 \(a→b\) も置きかえていきます。
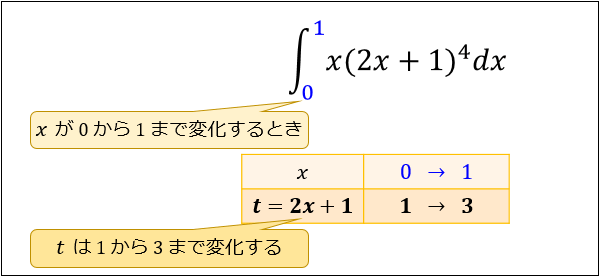
手順はカンタンで、\(t=2x+1\) の \(x\) に \(a,b\) を代入するだけ。
例題では積分区間が \(x:0→1\) なので、\(t:1→3\) に置きかわります。
Step④ \(x,dx\) を \(t,dt\) に変換する
さて、これで\(「x=\dfrac{t-1}{2}」\)\(「dx/dt=\dfrac{1}{2}」\)\(「t:1→3」\)という3つのパーツが集まりました。
ここからが置換積分の本番です。
今まで集まった3つのパーツを使って、\(x,dx\) を \(t,dt\) に変換していきましょう。
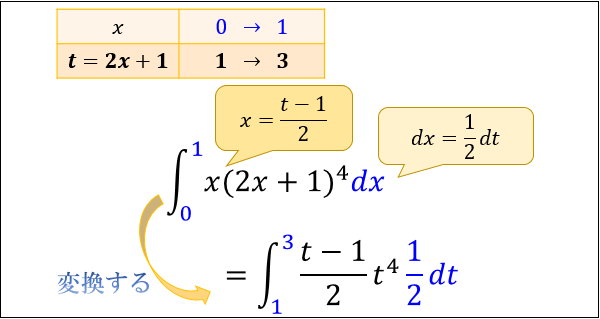
(1): \(x\) を \(\dfrac{t-1}{2}\) に(\(2x+1\) を \(t\) に)
(2): \(dx\) を \(\dfrac{1}{2}dt\) に
(3): 積分区間 \(x:0→1\) を \(t:1→3\) に
こうすることで \(t\) のカンタンな積分式になり、積分の公式を当てはめやすくなります。
Step⑤ 積分の公式を使ったうえで、求められた答えの形にする
\(t\) のカンタンな積分式になったら、積分の公式を使って計算していきます。
まずは不定積分 $\displaystyle \int x(2x+1)^4 dx$ の場合。

\(t\) は自分で置いた値なので、答えとしては適切ではありません。
そのため、\(t=2x+1\) を代入して求められた形式である「\(x\) の式」に戻す必要があります。
つぎは定積分 $\displaystyle \int_0^1 x(2x+1)^4 dx$ の場合。

定積分は、積分範囲も変換されているので \(x\) に戻さずに直接答えを計算してOK
最後の行の計算では、分母が同じ値どうしを先に計算したほうが良いです。
まとめ
- Step① \(=t\) に置きかえるものを決める
- Step② \(x=g(t)\) の形に変換して \(t\) で微分。\(dx/dt\) を求める
- Step③ 定積分なら積分区間 \(a→b\) も置きかえる
- Step④ \(x,dx\) を \(t,dt\) に変換する
- Step⑤ 積分の公式を使ったうえで、求められた答えの形にする