\(n\) 個のデータ \((x_1,y_1),(x_2,y_2),\)\(\cdots,(x_n,y_n)\) について、「\(x\) と \(y\) の共分散」を「\(x\) の標準偏差と \(y\) の標準偏差の積」で割った値のことを、\(x\) と \(y\) の相関係数と言います。

相関係数は、\(x\) と \(y\) の間の直線的な関係性の強さを表す指標です。
「年齢 \(x\) が高いほうが、年収 \(y\) も高い傾向がある」
「親の身長 \(x\) が高いほうが、子供の身長 \(y\) も高い傾向がある」
「勉強時間 \(x\) が長いほうが、学力 \(y\) も高い傾向がある」
世の中にはこういった傾向が数多く存在しますが、これらはあくまで『傾向』であって、「45才の人の年収が絶対に25才の人の年収よりも高い」という訳ではありません。
年齢も親の身長も勉強時間も、ある程度の目安でしかないんです。
ただ、皆さんはこういった話を聞いたときに「ある程度って具体的にどの程度なんだ?」と疑問に思ったことはありませんか?
この「ある程度」が具体的にどの程度なのかを数値化したもの。それが、相関係数です。
今回は、相関係数の求め方と使い方について解説していきます。
相関係数とは
相関係数とは、2種類のデータの(直線的な)関係性の強さを \(-1\) から \(+1\) の間の値で表した数のこと。記号では \(ρ\) や \(r\) で表される値です。
\(ρ\) は母集団の相関係数(例:日本全体での身長と体重の関係性)
\(r\) は標本の相関係数(例:今回得られたデータ内での身長と体重の関係性)
を指すことが多いです。
相関係数は一般的に、\(+1\) に近ければ近いほど「強い正の相関がある」、\(-1\) に近ければ近いほど「強い負の相関がある」、\(0\) に近ければ近いほど「ほとんど相関がない」と評価されます。

相関係数は \(x\) と \(y\) の直線的な関係性の強さを調べるのに使います。
ここからは相関係数を通じて色んな直線的な関係性の強さを見ていきましょう。
正の相関
相関係数が \(+1\) に近い値の場合、「\(x\) と \(y\) には正の相関がある」といって「\(x\) が大きいとき、\(y\) も大きい傾向がある」ことを意味します。
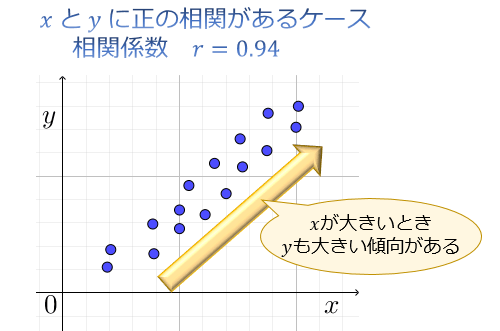
下図は、相関係数 \(r=0.94\) の強い正の相関があるケース。
「\(x\) が大きいとき、\(y\) も大きい傾向がある」のが分かりますね。
負の相関
一方、相関係数が \(-1\) に近い値の場合、「\(x\) と \(y\) には負の相関がある」といって「\(x\) が大きいとき、\(y\) は小さい傾向がある」ことを意味します。
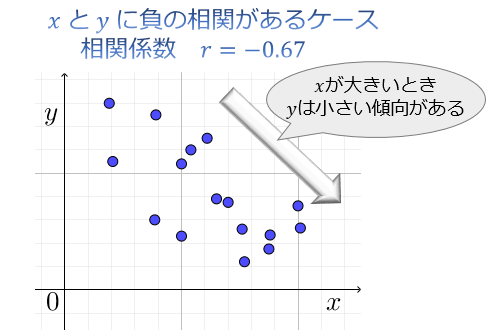
下図は、相関係数 \(r=-0.67\) の負の相関があるケース。
「\(x\) が大きいとき、\(y\) は小さい傾向がある」のが分かります。
相関がない
最後に、相関係数が \(0\) に近い値の場合、「\(x\) と \(y\) にはほとんど相関がない」といって「\(x\) の大小は \(y\) の大小と直線的な関係がない」ことを意味します。
この場合、「直線的な関係がない(比例していない)」だけで何らかの関連性がある可能性は否定できないので、グラフと見比べながら判断する必要があります。
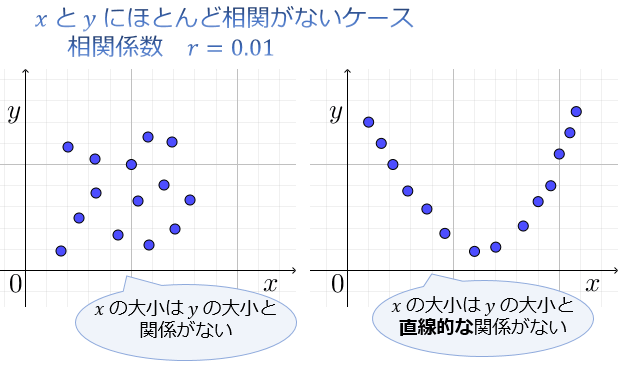
下図は、どちらも相関係数 \(r=0.01\) のほとんど相関がないケース。
左は \(x\) と \(y\) に関連性がなく、右は関連性はあるが直線的ではないため相関係数が \(0\) に近い。
共分散と標準偏差から相関係数を求めてみよう

ここからは、実際に相関係数を求めてみましょう。
ある日、Aさん,Bくん,Cくん,Dさんの4人は100マス計算のテストを受けた。
下の表は、4人の「テストの点数・テストを終えるまでにかかった所要時間・前日の勉強時間・身長・答案用紙の空欄の数」を表している。
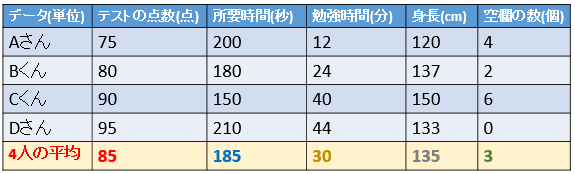
相関係数の公式は「\(x\) と \(y\) の共分散」を「\(x\) の標準偏差と \(y\) の標準偏差の積」で割った値です。
そこでまずは、\(x\) と \(y\) の共分散から求めてみましょう。
\(x\) と \(y\) の共分散は、「\(x\) の偏差」と「\(y\) の偏差」の積の平均で求められます。
※偏差:平均との差 \((x_i-\overline{x})\) のこと

このように計算すると
点数 \(x\) と所要時間 \(y\) の共分散が \(-12.5\) (点×秒)
点数 \(x\) と勉強時間 \(y\) の共分散が \(100\) (点×分)
点数 \(x\) と身長 \(y\) の共分散が \(48.75\) (点×cm)
点数 \(x\) 空欄の数 \(y\) の共分散が \(-5\) (点×個)
であることがわかります。
次に、\(x\) の標準偏差と \(y\) の標準偏差を求めます。
\(x\) の標準偏差は、「\(x\) の偏差」の2乗の平均の正の平方根で求められます。

このように計算すると
点数の標準偏差が \(\sqrt{62.5}≒7.905\) (点)
所要時間の標準偏差が \(\sqrt{525}≒22.912\) (秒)
勉強時間の標準偏差が \(\sqrt{164}≒12.806\) (分)
身長の標準偏差が \(\sqrt{114.5}≒10.700\) (cm)
空欄の数の標準偏差が \(\sqrt{5}≒2.236\) (個)
であることがわかります。
最後に、先ほどの「共分散」を対応する「2つの標準偏差の積」で割ると
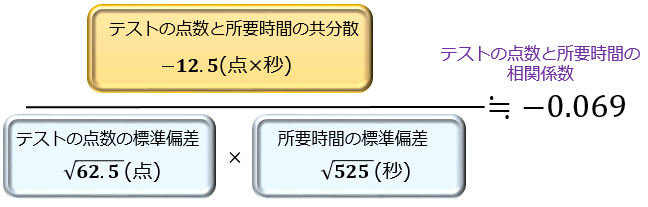
見事、相関係数が求まりました。

エクセルのCORREL関数で確認してみよう
共分散・標準偏差・相関係数は、計算量が多くなりやすいので、それだけケアレスミスもよく起こります。
そのため、これらを求める際にはEXCELを利用するのがオススメです。
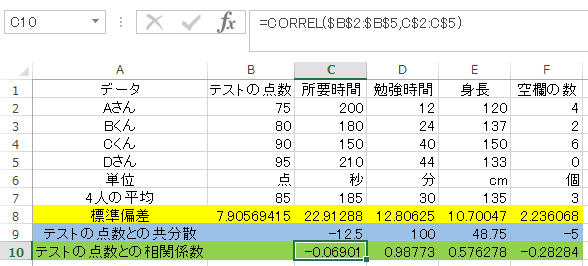
標準偏差はSTDEV.P関数
共分散はCOVAR関数
相関係数はCORREL関数
を使います。
3つの注意点
相関係数は \(x\) と \(y\) の関係性の強さを数値化するのに便利な指標ではありますが、万能というわけではなく、使用するうえではいくつか注意点があります。
①少ないデータからの相関係数はあまり意味をなさない
今回は相関係数 \(r\) の求め方をカンタンに説明するために、生徒数 \(n=4\) という少ないデータで相関係数を計算しました。
ただ、実務においてはこのような「少ないデータから得られた相関係数 \(r\) 」はあまり意味を成さないということを覚えておいてください。
たった4人のデータから求められた「テストの点数と空欄の数の相関係数」 \(r=-0.2828\) からは「この4人のデータ内に限って言えば、テストの点数と空欄の数には弱い負の相関があるように見える」と言えるに過ぎません。
それを一般化して「テストの点数と空欄の数には弱い負の相関がある」と言うのは早計です。
なぜなら、母集団の相関係数 \(ρ=0\) であっても標本の選ばれ方から偶然「今回のような相関係数 \(r\) 」が得られた可能性があるからです。
実務において相関関係の度合いを判断するときは、十分な量 \((n\geqq100)\) のデータから算出した相関係数を使って判断するようにしましょう。
一般的には、相関係数 \(r\) とデータの総数 \(n\) から算出した「p値」が \(0.05\) より小さい時に「有意な相関がある」と言います。
②外れ値に弱い
「共分散」を「2つの標準偏差の積」で割った値で求められる相関係数は、データが正規分布を始めとした特定の分布に従うことを前提としています。
裏を返せば、こういった分布に従わず「外れ値」が出てくるようなデータから求めた相関係数は、「外れ値」の影響を大きく受けてしまい、正確な測定ができなくなってしまうという弱点があるんです。
「外れ値」が出てくるようなデータでは、ノンパラメトリック法(スピアマンの順位相関係数など)を利用したほうが良いでしょう。
③相関関係があるからといって因果関係があるとは限らない
相関係数についてよくある誤解が、相関関係と因果関係の混同です。
例えば、生徒数 \(n=200\) のデータから算出された「身長と100マス計算テストの点数の相関係数」が \(r=0.57\) だったとしましょう。
この場合「身長が高い生徒ほどテストの点数が高い傾向がある(正の相関がある)」ということになりますが、だからと言って「身長が高いからテストの点数が良くなった(因果関係がある)」とは考えにくいですよね。
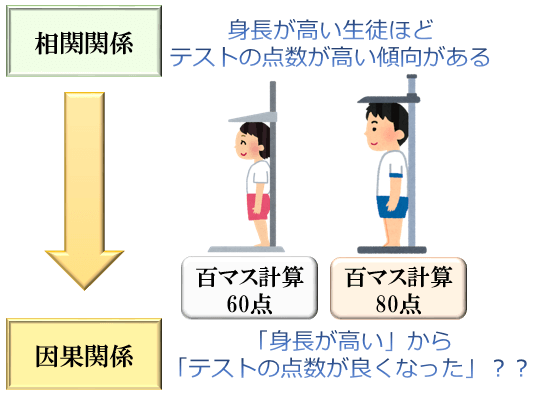
このケースでは「高学年の生徒だから身長が高い」という因果関係と「高学年の生徒だから100マス計算テストの点数が良い」という因果関係によって「身長とテストの点数の間に正の相関ができた」と考えるのが妥当です。
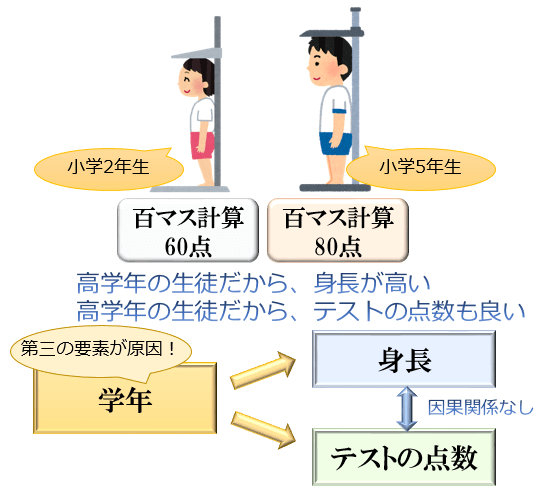
このように、「\(x\) と \(y\) の間に相関関係があったとしても \(x\) と \(y\) の間に因果関係があるとは限らない(第三の要素 \(z\) が原因となっている可能性がある)」ということを覚えておいてください。
相関関係と因果関係の違いについては「相関関係と因果関係の違い」の記事でさらにくわしく解説しているので、参考にしてみてください!