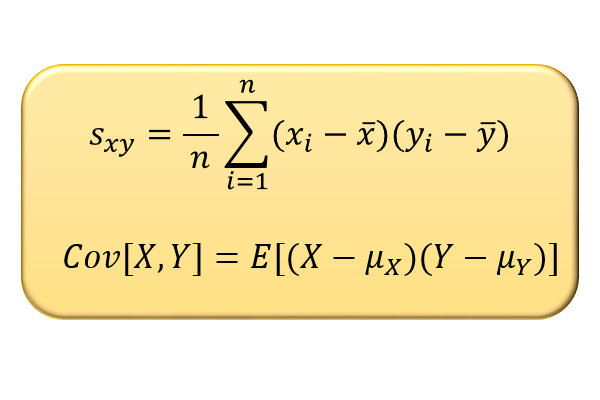
共分散とは2つの変数の関係を表す値で、「平均値からの偏差の積の平均」で求められます。
共分散は「身長と体重」のような2変数データの関係性を表したり、「事象Xが起こるときに事象Yも起こる傾向があるか」のように2つの確率変数の関係性を表すのに使います。
n個の2変数データの共分散
\(n\) 個のデータ \((x_1,y_1),(x_2,y_2),\)\(\cdots,(x_n,y_n)\) に対して、以下の式で表される値 \(s_{xy}\) を共分散と言います。

実際に以下の4人 \(A,B,C,D\) の数学と国語の点数について、「数学と国語の点数の共分散」を求めてみましょう。
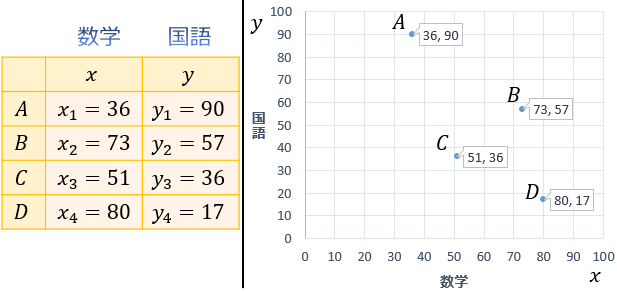
Step①xとyの平均を求める
まず、\(x\) の平均と \(y\) の平均を求めます。
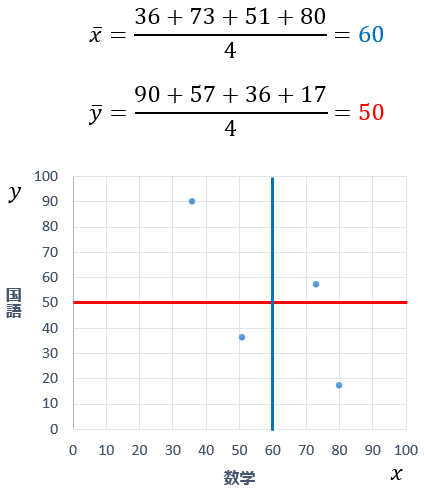
数学 \(x\) の平均点を青い線、国語 \(y\) の平均点を赤い線で表しています。
Step②各データのxの偏差とyの偏差の積を求める
次に、各データの「\(x\) の偏差」と「\(y\) の偏差」をそれぞれ求めます。
偏差とは、各データの値から平均値を引いた値です。
\(x\) の平均が \(60\) なので各 \(x_i\) から \(60\) を引き、 \(y\) の平均が \(50\) なので各 \(y_i\) から \(50\) を引くと…
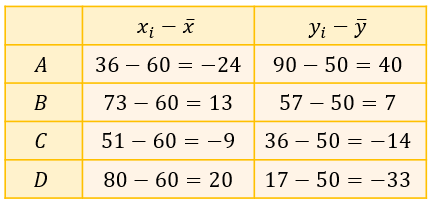
偏差が求まります。
すべての偏差が求まったら、「\(x\) の偏差」と「\(y\) の偏差」をそれぞれかけて積を求めましょう。

偏差の積は、上図のように「\(x\) の平均からの距離」×「\(y\) の平均からの距離」の面積をイメージすると理解しやすいです。
Step③積の合計をデータの総数で割る
最後に、求めた積をすべて足した後でデータの総数で割ると、共分散が求まります。
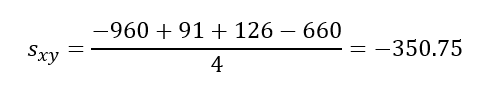
以上から、4人の「数学と国語の点数の共分散」が \(-350.75\) と求まりました。
2つの確率変数の共分散
次は、2つの確率変数 \(X\) と \(Y\) の共分散について。
\(n\) 個のデータが「確率分布」、平均が「期待値」に変わっただけで考え方は同じです。
2つの確率変数 \(X\) と \(Y\) の共分散は \(Cov[X,Y]\) または \(σ_{XY}\) と表記され、以下の式で与えられます。

共分散を求めるときは、次の公式を使うと計算が楽になります。

例題)サイコロを1回だけ振る。確率変数 \(X\) を「5の目が出た回数 + \(1\)」、確率変数 \(Y\) を「6の目が出た回数 + \(1\)」とする。このとき、\(X\) と \(Y\) の共分散は?
\(P(X=1,Y=1)\) は「5も6も出ない確率」なので、\(4/6\)
\(P(X=2,Y=1)\) は「5が出て、6が出ない確率」なので、\(1/6\)
\(P(X=1,Y=2)\) は「6が出て、5が出ない確率」なので、\(1/6\)
\(P(X=2,Y=2)\) は「1回しか振っていないのに5も6も出る」ことはありえないので、\(0\)
よって、\(X\)と \(Y\) の同時確率分布は以下の通りになります。
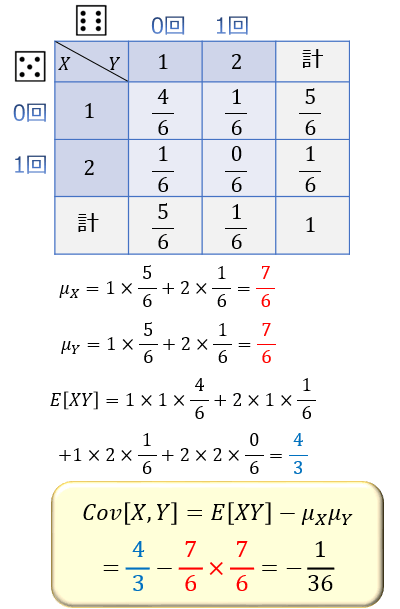
公式に当てはめることで、2つの確率変数 \(X\) と \(Y\) の共分散が \(-1/36\) と求まりました。
共分散の解釈と注意点
共分散は
正の値(プラス)なら「\(x\) が大きいとき、\(y\) も大きい傾向がある」
負の値(マイナス)なら「\(x\) が大きいとき、\(y\) は小さい傾向がある」
ことを意味します。
テストの例では「(今回のテストでは)数学の点数が高い人ほど国語の点数は低い傾向がある」
サイコロの例では「5の目を出した回数が多いほど、6の目を出した回数は少ない傾向がある」
と解釈できます。
共分散を使うときは、1つ注意点があります。
それは、共分散には「2つの変数の関係の強さ」と「単位」の両方の影響を受けてしまう欠点があるということ。
そのため、共分散の値の意味をキチンと解釈したい場合には「共分散を各変数の標準偏差の積で割る」ことにより、単位の影響を取り除いた相関係数を使うのが一般的です。





