数学の疑問部分積分法の公式の証明と「くり返し部分積分」のやり方
2018年3月27日 Tooda Yuuto アタリマエ！
このページでは、部分積分法の公式の証明と「部分積分をくり返し行うタイプの問題」の解き方を解説していきます。 (さらに&h …
数学の疑問部分積分の解き方とコツ。どっちを微分するか判断するポイントとは？
2018年3月24日 Tooda Yuuto アタリマエ！
関数 \(f(x),g(x)\) とそれらを微分した \(f'(x),g'(x)\) に対して成立する以下の公式を、部分積分と言いま …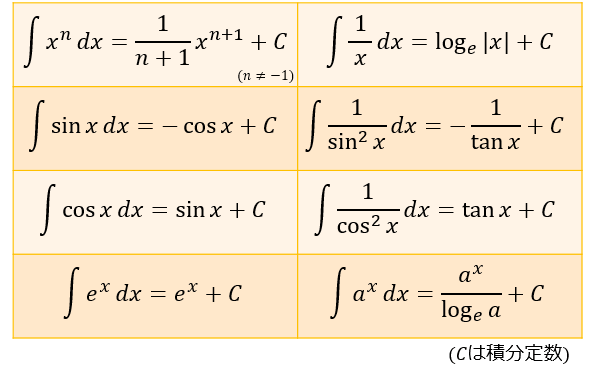
数学の疑問積分の公式一覧
2018年3月19日 Tooda Yuuto アタリマエ！
このページでは、よく使う積分の公式をまとめています。 (さらに…) …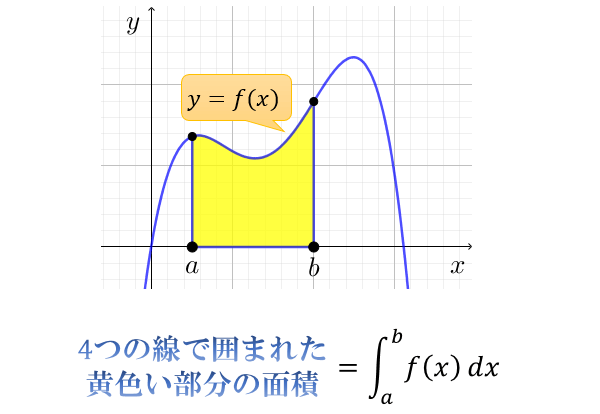
数学の疑問積分とは何なのか？面積と積分計算の意味
2018年3月17日 Tooda Yuuto アタリマエ！
積分とは「微分の反対」に相当する操作で、関数 \(f(x)\) を使って囲まれた部分の面積を求めることを意味します。 例えば $\displaystyle \ …
数学の疑問積分のやり方と基礎公式。不定積分と定積分の違いとは？
2018年3月8日 Tooda Yuuto アタリマエ！
積分とは、「微分の反対」に相当する操作です。 たとえば、\(F(x)=3x^2\) を微分すると \(F'(x)=6x\) に …
数学の疑問因数分解の公式まとめ一覧とその活用例
2018年3月8日 Tooda Yuuto アタリマエ！
この記事では、因数分解の公式とその活用例をまとめています。 因数分解2乗の公式 特に重要なのが、④の公式です。
④の公式に \(a=y,b=y\) を …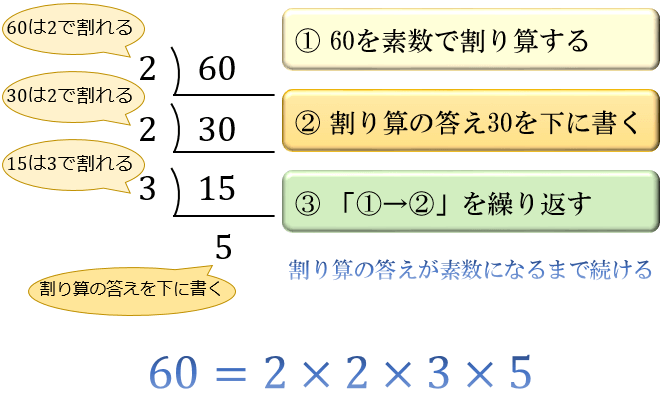
数学の疑問素因数分解のやり方。5つのステップで分かる素因数分解問題の解き方とコツ
2018年2月15日 Tooda Yuuto アタリマエ！
ある整数を「素数のかけ算」の形に変形することを素因数分解(prime factorization)と言います。 たとえ …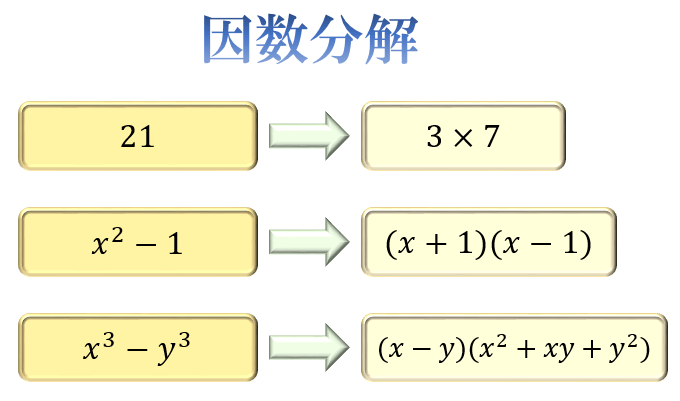
数学の疑問因数分解の問題の解き方とコツ。2乗・3乗公式とたすきがけ
2017年11月8日 Tooda Yuuto アタリマエ！
数の中には「2つ以上の数のかけ算」に変形できるものがたくさんあります。
例えば \(x^2-1\) は \((x+1)(x-1)\ …
数学の疑問ルート２ルート３ルート５ルート７のゴロ合わせ【素数の平方根の筆算の仕方】
2017年11月1日 Tooda Yuuto アタリマエ！
\(\sqrt{2}=1.41421356\cdots\) は「一夜一夜に人見頃」と覚えます。
これは「一晩経つごとに桜の花が開い …
数学の疑問有理数と無理数の違い。ルート２が無理数であることの証明
2017年10月23日 Tooda Yuuto アタリマエ！
今回は、有理数と無理数について。 有理数は英語で Rational Number 、無理数は英語で Irrational Nu …
数学の疑問べき乗とは何か。ゼロ乗・マイナス乗・分数乗・無理数乗ってどういう意味？
2017年10月20日 Tooda Yuuto アタリマエ！
\(2^3\) や \(3^4\) に限らず、\(3^{-2}\)・\(5^\frac{1}{2}\)・\(8^π\) といった値も …
数学の疑問累乗とは。その意味と計算方法を解説【底・指数とは何か】
2017年10月18日 Tooda Yuuto アタリマエ！
同じ数をくり返しかけ算したもののことを、累乗と言います。
たとえば \(3\) を \(4\) 回かけ合わせた場合、\(3×3×3×3 …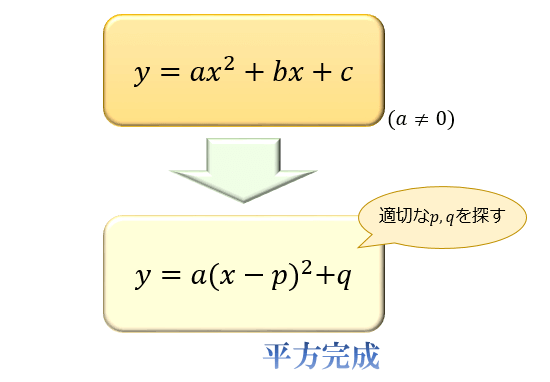
数学の疑問平方完成のやり方と平方完成するメリットについて
2017年10月10日 Tooda Yuuto アタリマエ！
\(ax^2+bx+c\) の形の二次式を \(a(x-p)^2+q\) の形に変形することを平方完成と言います。 \(m …
数学の疑問フィボナッチ数列とは。一般項の証明・黄金比との関係について
2017年10月6日 Tooda Yuuto アタリマエ！
フィボナッチ数列は「隣り合う2つの数を合計すると次の数になる数列」です。
英語では Fibonacci Sequence. 名前の …