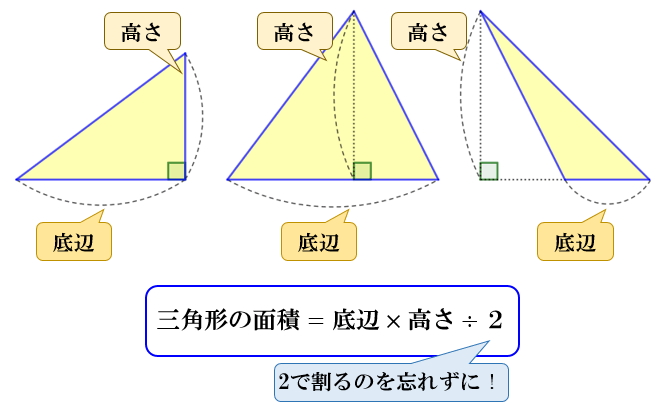
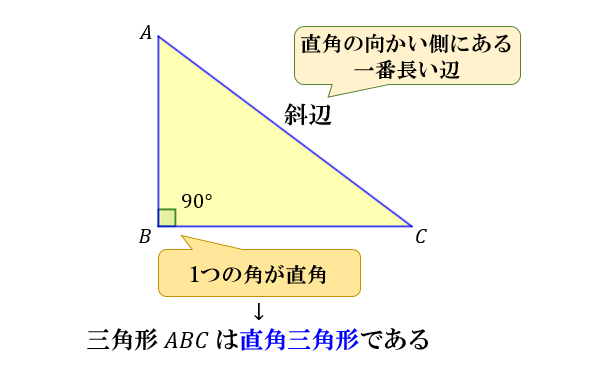
ヘロンの公式とは、三角形の3辺の長さ \(a,b,c\) を使って素早く三角形の面積を求める公式です。
\(S=\sqrt{s(s-a)(s-b)(s-c)}\)
\(\left(ただし、s=\dfrac{a+b+c}{2}\right)\)
で求められる
たとえば、「3辺の長さが \(7,6,5\) の三角形」の面積 \(S\) は
\(s=\dfrac{7+6+5}{2}=9\) から
\(S=\sqrt{9×(9-7)×(9-6)×(9-5)}\)
\(=6\sqrt{6}\)
と求められます。
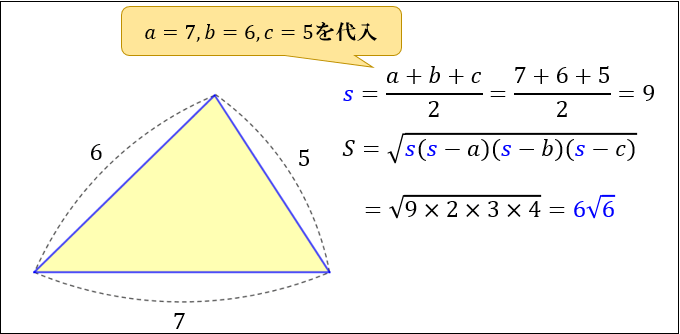
このページでは、このヘロンの公式の仕組みを図を使ってみていきましょう。
ヘロンの公式の図解
ヘロンの公式は、三角形 \(ABC\) の内接円 \(O\) と傍接円 \(O’\) を使って示すことができます。
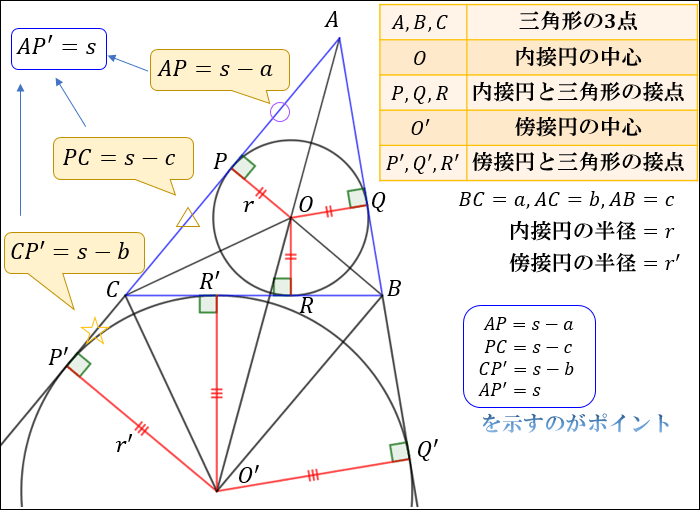
内接円:三角形の3辺すべてと接する円
傍接円:①\(AB\) の延長線 ②\(AC\) の延長線 ③\(BC\) の3つすべてと接する円
6つのステップに分けてみていきましょう。
Step① 内接円の性質から \(S=sr\)
まず、下図のように「三角形の内接円の中心 \(O\)」を中心に三角形を3分割します。
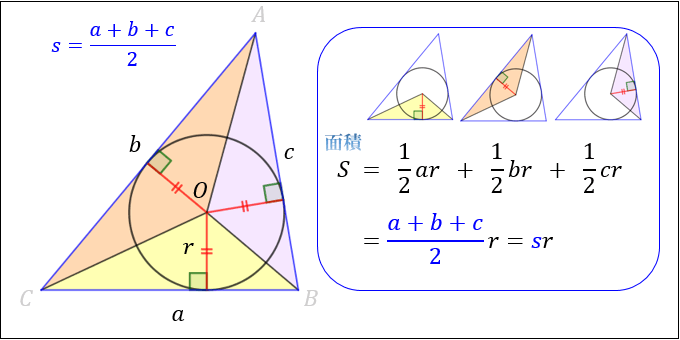
円は接線と「接点で垂直に交わる」ので、これら3つの小さな三角形はそれぞれ
底辺 \(a\)、高さ \(r\) の三角形
底辺 \(b\)、高さ \(r\) の三角形
底辺 \(c\)、高さ \(r\) の三角形
になることが分かります。
よって、三角形 \(ABC\) の面積 \(S\) は
\(S=sr\cdots(1)\)
で表されることが分かります。
Step② \(s-a\),\(s-b\),\(s-c\) を見つける
次に、直角三角形 \(APO,AQO\) に対して三平方の定理を使うと、 \(AP=AQ\) が成り立ちます。
同様に、\(BQ=BR\)、\(CR=CP\) も成立します。
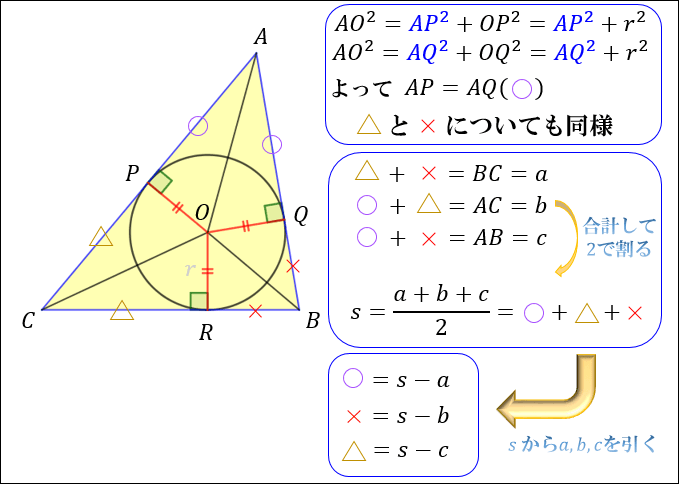
これらを \(○,×,△\) とおくと、三角形の3辺の和が「 \(○+△+×\) のちょうど2倍」になることが分かるので
\(s=○+△+×\) が成立。
\(s\) から各辺を引くことで
\(○=s-a\)
\(×=s-b\)
\(△=s-c\)
になることが分かります。
Step③ \(AP’=s\) を示す
次に、傍接円 \(O’\) について三平方の定理を使うと
\(CP’=CR’,BQ’=BR’,AP’=AQ’\) が成り立つことが分かります。
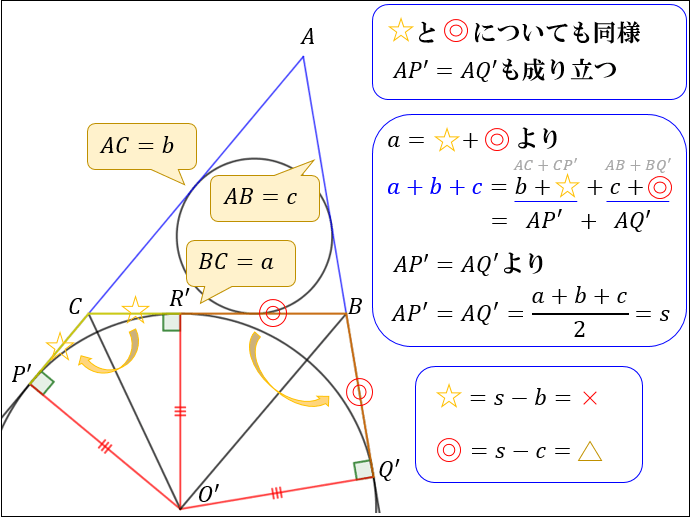
これらを使って上のように変形していくことで、
\(AP’=s,CP’=s-b\) になることが分かります。
Step④ \(△APO\) と \(△AP’O\) の相似
重要な線の長さが分かったら、次は直角三角形 \(△APO,△AP’O’\) に注目しましょう。
これら2つは共通する角 \(∠A\) をもつ直角三角形なので、3角の大きさが等しく、相似関係にあります。
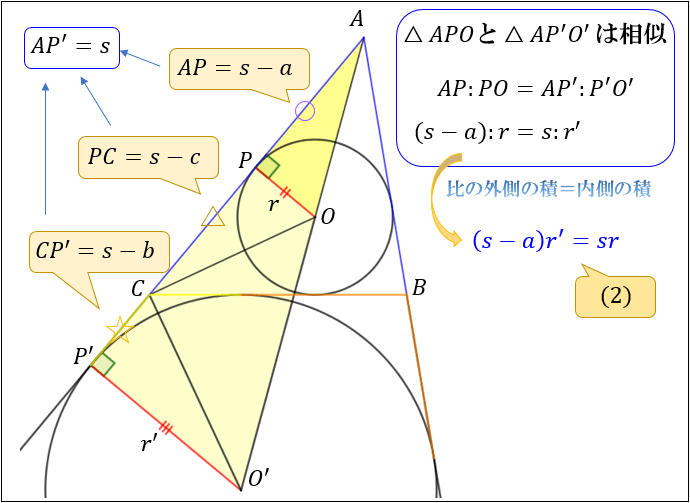
相似な三角形の性質「対応する線分の長さの比は等しい」より
\(AP:PO=AP’:P’O’\) から \((s-a):r=s:r’\)
比の「内項の積」と「外項の積」は等しいので
\((s-a)r’=sr\cdots(2)\)
が求まります。
Step⑤ \(△COP\) と \(△O’CP’\) の相似
今度は直角三角形 \(△COP,△O’CP’\) に注目すると、下図のように相似関係にあることが分かります。

さきほどと同様に
相似な三角形の性質「対応する線分の長さの比は等しい」より
\(PC:PO=P’O’:CP’\) から \((s-c):r=r’:(s-b)\)
比の「内項の積」と「外項の積」が等しいことから
\((s-b)(s-c)=rr’\cdots(3)\)
が求まりました。
Step⑥ (1),(2),(3) を解く
最後に、Step①,④,⑤で求まった3つの式をつなげてみましょう。
\(S=sr\cdots(1)\)
\((s-a)r’=sr\cdots(2)\)
\((s-b)(s-c)=rr’\cdots(3)\)
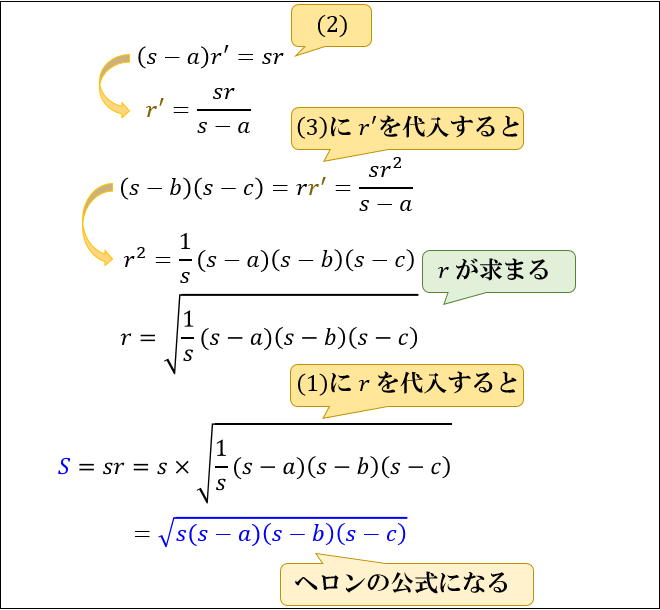
ヘロンの公式が求まりました。
三角関数を用いた証明
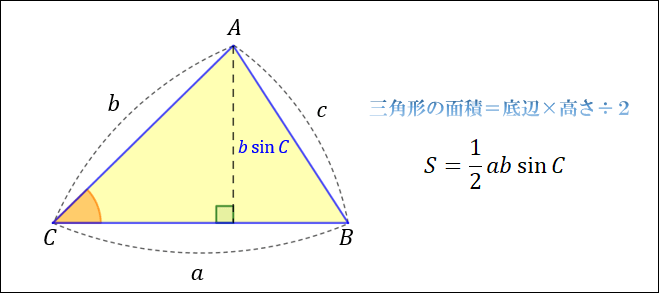
ヘロンの公式は
の3つを使うと手早く証明することができます。