このページでは、部分積分法の公式の証明と「部分積分をくり返し行うタイプの問題」の解き方を解説していきます。
部分積分法の公式の証明
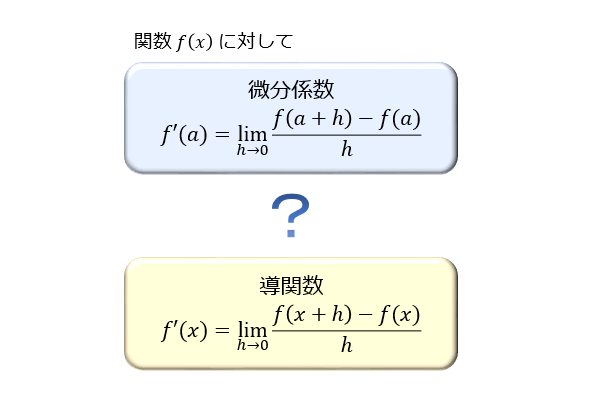
関数 \(f(x),g(x)\) とそれらを微分した \(f'(x),g'(x)\) に対して
部分積分法の公式は以下のように表されます。
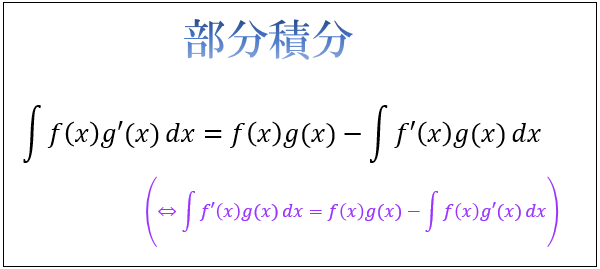
部分積分法の公式は、積の微分法の公式から求められます。
【積の微分法の公式】
\( \{ f(x)g(x) \}’=f'(x)g(x)+f(x)g'(x)\)
例)\(\{x\sin{x}\}’=\sin{x}+x\cos{x}\)
この式の両辺を積分してから左辺と右辺を整理すれば、部分積分法の公式が求まります。

xの2乗と対数関数の積分
ここからは、前回の記事よりも難しい部分積分の問題を見ていきましょう。
問①.$\displaystyle \int x^2 \log_e{x}\ dx$ を求めて下さい。
\(\log_e{x}\) を含むかけ算の部分積分では、\(\log_e{x}\) を微分に回して \(\dfrac{1}{x}\) を作ります。

このように、\(x^n\) と対数関数の組み合わせでは対数を微分に回すことで \(x^n\) と \(1/x\) の相殺を狙うのがポイントです。
xの2乗と三角関数の積分
問②.$\displaystyle \int x^2 \cos{2x}\ dx$ を求めて下さい。
微分したら元よりカンタンになるのは \((x^2)’=2x\) なので、\(f(x)=x^2\)
積分してもあまり複雑にならないのは \(\int \cos{2x} dx=\dfrac{\sin{2x}}{2}\) なので、\(g'(x)=\cos{2x}\)
これを部分積分の公式に当てはめると、以下のように求まります。

部分積分して出てきた \(\int x \sin{2x}\ dx\) は2つの関数 \(x\) と \(\sin{2x}\) のかけ算ですよね。
そこで、これをさらに部分積分していきます。
このように、\(x^n\) と三角関数の組み合わせではカンタンな積分になるまで部分積分をくり返すのがポイントです。
カッコを開くときにプラス・マイナスを間違えないように慎重に計算しましょう。
指数関数と三角関数の積分(部分積分のループ)
問③.$\displaystyle \int e^x \sin{x}\ dx$ を求めて下さい。
\(e^x\) と \(\sin{x}\) の組み合わせは、少し特殊です。
\(e^x\) は何回積分しても \(e^x\) のまま
\(\sin{x}\) は何回微分しても \(\cos{x}\) と \(\sin{x}\) をループする
この組み合わせでは「カンタンな積分になるまで部分積分をくり返そう」と思っても、永遠に終わりません。
こういうループが起きるときは、求めたい式 \( \int e^x \sin{x}\ dx=I\) とおくのがコツです。

部分積分を進めていくと、右辺からも \(I=\int e^x \sin{x}\ dx\) が見つかります。
そこで、この \(I\) を左辺に移行すると
\(2I=e^x \sin{x}-e^x \cos{x}\) となります。
求めたいのはその半分 \(I\) なので、\(I=\dfrac{1}{2}(e^x \sin{x}-e^x \cos{x})+C\) が答えとなります。
対数関数の累乗の積分
問④.$\displaystyle \int (\log_e{x})^3\ dx$ を求めて下さい。
\(\log_e{x}\) を含む部分積分では、\(\log_e{x}\) を微分するのがコツ。
今回は \((\log_e{x})^3\) なので、一度部分積分しただけでは \(\int (\log_e{x})^2\ dx\) が残ります。
そこで \(\int (\log_e{x})^2\ dx\) をさらに部分積分し、 \(\int \log_e{x}\ dx\) まで落とし込みます。

計算量が非常に多くなってしまうので、対数関数の積分公式
$\displaystyle \int \log_e{x}\ dx=x\log_e{x}-x+C$
を暗記しておくのがオススメです。