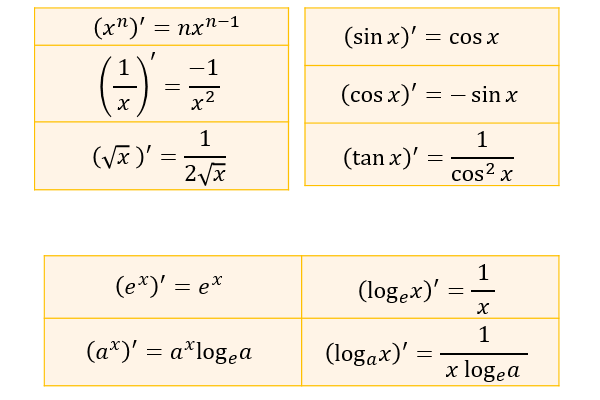
このページでは、よく使う微分の公式をまとめています。
微分(導関数)の定義式
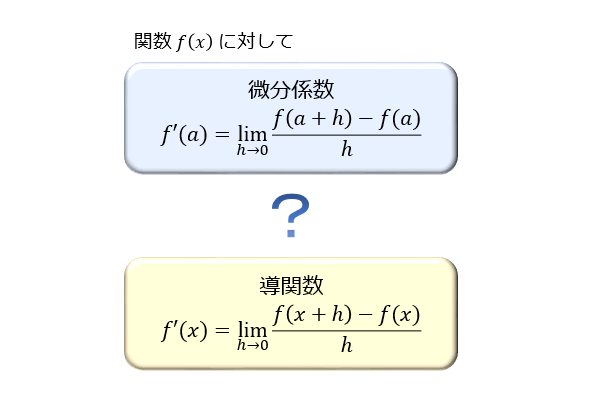
関数 \(f(x)\) に対して、導関数 \(f'(x)\) は以下の式で定義される
● $\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} $
式の考え方は「微分とは何かを分かりやすくするコツは速度にある」を参照
xのn乗の微分公式
● \((x^n)’=nx^{n-1}\) (\(n\) は実数)
最も基本となる公式
● \(\left(\dfrac{1}{x}\right)’=-\dfrac{1}{x^2}\)
● \((\sqrt{x})’=\dfrac{1}{2\sqrt{x}}\)
\((x^n)’=nx^{n-1}\) に \(n=-1\) や \(n=\dfrac{1}{2}\) を代入すると求まる
定数倍の微分公式
● \((a)’=0\) (\(a\) は実数)
● \((ax)’=a\)
● \((a\cdot f(x))’=a\cdot f'(x)\)
例: \((5x^3)’=5×3x^{3-1}=15x^2\) \((7x^4)’=7×4x^{4-1}=28x^3\)
三角関数の微分公式
● \((\sin x)’=\cos x\)
● \((\cos x)’=-\sin x\)
● \((\tan x)’=\dfrac{1}{\cos^2 x}\)
指数関数の微分公式
● \((e^x)’=e^x\)
● \((a^x)’=a^x\log_{e}{a}\)
対数関数の微分公式
● \((\log_{e}{x})’=\dfrac{1}{x}\)
● \((\log_{a}{x})’=\dfrac{1}{x\log_{e}{a}}\)
● \((\log_{e}{|f(x)|})’=\dfrac{f'(x)}{f(x)}\)
\(\log_{e}{x}\) は自然対数。\(\log{x}\) と省略表記されることが多い
対数微分法
● \((x^x)’=(\log_{e}{x}+1)x^x\)
\(y=x^x\) の両辺の対数をとってから微分することで求まる
和・積・商の微分
\((a\cdot f(x)+b\cdot g(x))’=a\cdot f'(x)+b\cdot g'(x)\)
\(=2×3x^{3-1}+4×5x^{5-1}=6x^2+20x^4\)
\((f(x)\cdot g(x))’=f'(x)\cdot g(x)+f(x)\cdot g'(x)\)
\(=3x^2\sin{x}+x^3\cos{x}\)
\(\left(\dfrac{f(x)}{h(x)}\right)’=\dfrac{ f'(x)\cdot h(x)-f(x)\cdot h'(x) }{ \{{h(x)}\} ^2 }\)
合成関数の微分
● \(\{f(g(x))\}’=f'(g(x))g'(x)\)
例:\(\{\sin^3 {x}\}’=3\sin^2{x}(\sin{x})’=3\sin^2{x}\cos{x}\)
\(f(x)=x^3\) , \(g(x)=\sin{x}\)