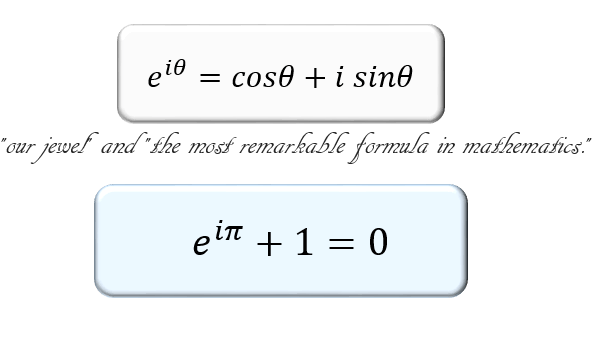
数学の三大分野である、幾何学・代数学・解析学。
図形の性質について研究する幾何学は、「円周の長さ ÷ 直径」として円周率 π を定義し、
方程式の解き方を研究する代数学は、「i × i =-1」となる数として虚数単位 i を定義し、
関数の極限や微分・積分について研究する解析学は、ネイピア数 e を定義しました。
全く関係のないところから出てきたこれら3つの値が、「eiπ + 1 = 0 」というシンプルな1つの式で繋がる。
それが、オイラーの等式です。
オイラーの公式とは
オイラーの等式を求めるにはまず、「オイラーの公式」を知る必要があります。
オイラーの公式とは、ネイピア数 e と三角関数 sinθ・cosθ (弧度法)の間に成り立つ以下の関係式のこと。
(※弧度法:半径1の円の、弧の長さθに対応する角度をθと定義する方法。単位はラジアンで、360度= 2π ラジアン)

この公式は、物理学者のリチャード・ファインマンによって「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」と評されたことで有名な公式です。
まずは、この「オイラーの公式」の式の意味を見ていきましょう。
ネイピア数 e
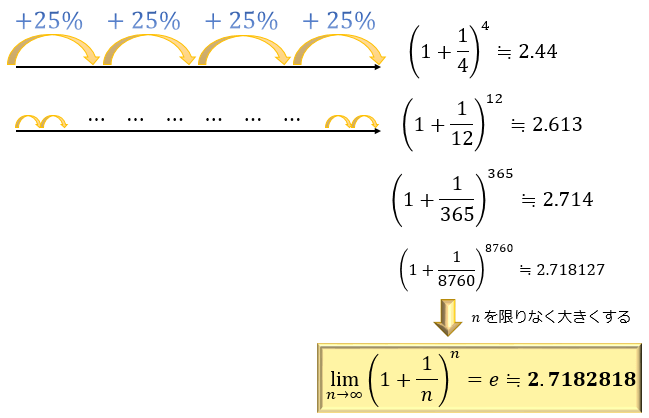
オイラーの公式の左辺に出てくるネイピア数 e は、2.71828…と無限に続く数です。

ネイピア数 e は、(1+1/n)のn乗の極限(n→∞)として求められます。
このネイピア数 e を x 乗した関数「 ex 」は指数関数と呼ばれており、微分した関数(導関数)も「 ex 」自身になるという特異な性質を持っていることから、微分・積分を扱う解析学において重要な役割を果たしています。
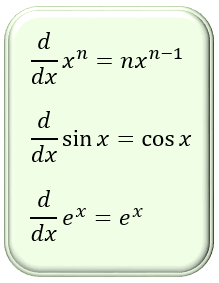
マクローリン展開
指数関数「 ex 」や三角関数「sin(x)・cos(x)」は、以下のような無限級数で表せることが分かっています。
この式を、マクローリン展開( 0 を中心としたテイラー展開)と言います。
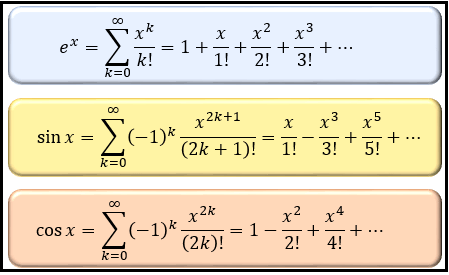

これら3つの式をよく見てみると、「 ex 」と「sin(x)+cos(x)」が非常によく似た形をしていることが分かりますよね。

ただ、そのままでは+と-で噛み合わない部分があるので、この2つの式を繋ぎ合わせるには一手間加える必要があります。
そこで登場するのが、虚数単位 i です。
虚数単位 i
虚数単位 i は、i × i =-1となる数。「-1の平方根」のことを指します。
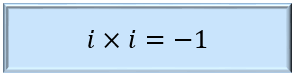
「円周の長さ ÷ 直径」や「すべての点で接線の傾きが y 座標と等しい関数」という形で現実で目にすることができる π や e と違い、 i は現実には存在しません。
ただ、「2乗したら-1になる」という性質が1つの数で座標を表したい時などに有用で、主に複素数平面という形で活用されている便利な「想像上の数」です。
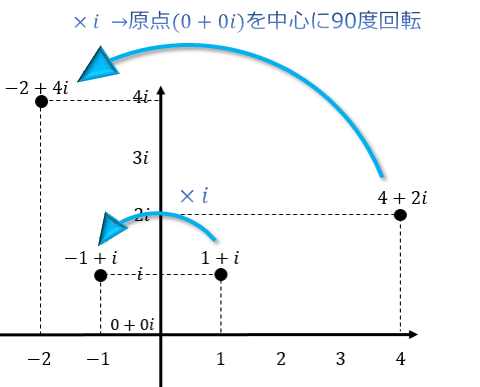

この「2乗したら-1になる」という性質に着目して
eiθ を「 ex 」のマクローリン展開の式の x を iθ で置き換えた式で定義し
三角関数「sin(x)、cos(x)」に x = θ を代入
sinθに i をかけると…

さきほどのマクローリン展開の式がつながって、「 eiθ = cosθ + i × sinθ 」の形に。
こうして求められるのが、オイラーの公式です。

円周率 π
最後に登場するのが、円周率 π。
「円周の長さ ÷ 直径」で表される、3.141592…と無限に続く数です。


オイラーの公式に θ = π を代入し、両辺に 1 を加えると…

「eiπ + 1 = 0 」というシンプルな式が導き出されました。
これが、オイラーの等式です。
オイラーの等式の美しさとは?
オイラーの等式は、解析学・代数学・幾何学という異なる分野において定義された全く起源の異なる3つの数「e,i,π」が、「1」と「0」という数学の基礎となる数とシンプルな1つの式で結び付けられることから、「数学史上最も美しい等式」としてよく取り上げられます。
数学という論理の世界で、美しさという「人によって感じ方の異なる概念」を定義づけるのは簡単なことではありませんが、少なくとも「この式に多くの数学者を惹きつける何かがある」のは間違いありません。
文学でいうところの「1つの小説の中に登場する、全く関係のない話だと思っていた3つの章の伏線が、最後の章で物語の軸と1本の線で結び付けられる」ような美しさを感じているのかもしれませんね。





