ある数 \(a\) を \(2\) 回かけ算することを「 \(2\) 乗する」と言い、\(a^2\) と書きます。
たとえば、
\(2\) を \(2\) 乗すると \(2^2=2×2=4\)
\(3\) を \(2\) 乗すると \(3^2=3×3=9\)
\(4\) を \(2\) 乗すると \(4^2=4×4=16\)
となります。
これに対して、「 \(2\) 乗すると \(x\) になる数」のことを「 \(x\) の平方根」と言います。
平方根は、英語では”square root”と言います。
たとえば、「 \(9\) の平方根」とは「 \(2\) 乗すると \(9\) になる数」を意味します。
今回は、そんな平方根の求め方・覚え方・他分野とのつながりを見ていきましょう。
平方根は「ボールを投げたときの放物線運動(二次方程式の解の公式)」や「株価の変動リスクの評価(標準偏差)」など、色んな分野の計算法が見えてくるので、理解できる世界がグッと広がってくる単元です。
ぼく自身、複雑にみえていた色んな数式を自分でも解けるようになって、数学の他分野への貢献度の高さに気づきだしたのはこの辺りからでした。
平方根の求め方
「 \(x\) の平方根」とは、「 \(2\) 乗したら \(x\) になる数」のことです。
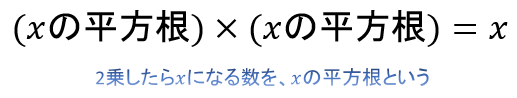
たとえば、「 \(9\) の平方根はいくつか?」という問題では 「 \(2\) 乗したら \(9\) になる数はいくつか?」を考えます。

「 \(2\) 乗したら \(9\) になる数」としては、 \(3\) と \(-3\) があります。

よって「 \(9\) の平方根は?」の答えは「 \(3\) と \(-3\) 」となります。
これらはまとめて \(±3\) と書いて、「プラスマイナス \(3\) 」と読みます。
【答え】 \(9\) の平方根は、\(±3\)
またこのとき、
プラスの「 \(3\) 」のことを「 \(9\) の正の平方根」
マイナスの「\(-3\)」のことを「 \(9\) の負の平方根」
と言います。
同じように
\(4\) の平方根は \(±2\)
\(16\) の平方根は \(±4\)
\(25\) の平方根は \(±5\)
\(100\) の平方根は \(±10\)
となります。
「2の平方根」は?
では次に、「 \(2\) の平方根」について考えてみましょう。
「 \(2\) 乗したら \(2\) になる数」は、いくつになるでしょうか?

\(1.4×1.4=1.96\)
\(1.5×1.5=2.25\)
なので、「 \(2\) の正の平方根」は \(1.4\) よりも大きくて \(1.5\) よりも小さいことが分かりますね。
実は、「 \(2\) の正の平方根」は \(1.4142\cdots\) と無限につづく数であることが分かっています。
ちょうど、円周率が3.1415…と無限に続いていくのと同じように。

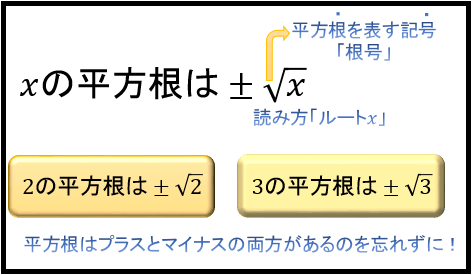
こういったケースでは、無限に続く数を書くわけにはいかないので、\(「\sqrt{}」\) で表される「根号」と呼ばれる記号を使って
「 \(2\) の平方根は \(±\sqrt{2}\) 」と表記します。

平方根の小数表記の覚え方と使い道
数学の世界では、「 \(2\) の平方根は?」と聞かれたら \(±\sqrt{2}\) と答えればOKです。
一方、物理学や統計学の世界では「 \(\sqrt{2}\) mとは具体的に何mなのかを小数を使って表したいケース」が多いので、\(\sqrt{2},\sqrt{3},\sqrt{5}\) の値を何桁か覚えておくと便利です。
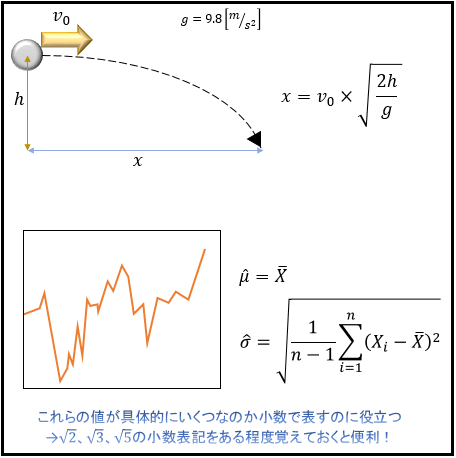
ここでは、\(\sqrt{2},\sqrt{3},\sqrt{5}\) の有名なゴロ合わせを見ていきましょう。
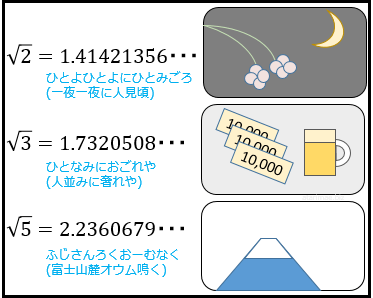
まず、\(\sqrt{2}\) の覚え方は『ひとよひとよにひとみごろ』。
一晩経つごとに、どんどんと桜が「人が見てちょうどよい頃合い(見頃)」になっていく様子を表す、風流なゴロ合わせとなっています。
\(\sqrt{3}\) の覚え方は『ひとなみにおごれや』。ケチな人に対して「もう少し奢れや!」とせまる、豪快なゴロ合わせです。
\(\sqrt{5}\) の覚え方は『ふじさんろくおーむなく』。富士山の麓(山の下の方の部分)でオウムが鳴いている様子を表しています。俳句にありそうな一文ですね。
次のページでは \(\sqrt{7}\) 以上の平方根のゴロ合わせも紹介しています。

「-1の平方根」は?
\(4×4=16\)、\((-4)×(-4)=16\) のように、正の数も負の数も2乗したら正の数になります。
そのため、\(-1\) や \(-16\) などの「負の数」には平方根が存在しません。
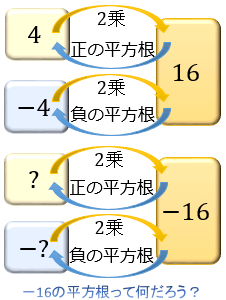
そのため、中学数学では負の数の平方根は「なし」で正解です。
ただし、高校以上の数学では「 \(i\) 」という「 \(-1\) の平方根」が存在する、という前提で話が進んでいく単元も出てきます。
これについては、「虚数とは何か?複素数とは何か?が一気に分かりやすくなる記事」で解説しています。

平方根の計算方法
平方根の意味が分かったら、次は平方根の計算です。
次のページでは、平方根の計算の仕方を見ていきましょう。