「3つの角のうち、1つの角が直角の三角形」のことを、直角三角形(英語では right triangle)と言います。
また、直角の向かい側にある一番長い辺のことを、斜辺と言います。

このページでは、直角三角形がもつ性質(面積・斜辺の長さの求め方・合同条件)を見ていきましょう。
直角三角形の面積
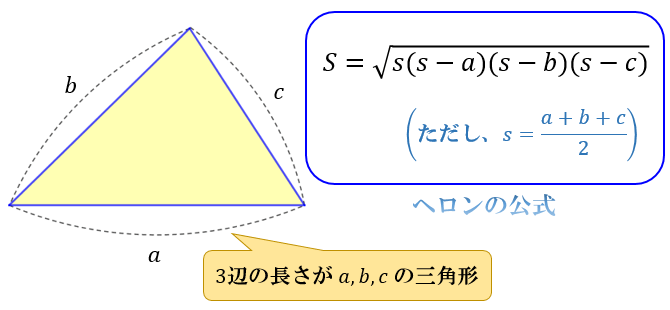
三角形の面積は\(「底辺×高さ÷2」\)という公式から求められます。
三角形の「高さ」の定義は「底辺に含まれない頂点から底辺におろした垂線の長さ」
「底辺」と「高さ」は \(90°\) に交わる
直角三角形では、直角をはさむ2つの辺の片方を「底辺」としたら、もう片方の辺が「高さ」になります。
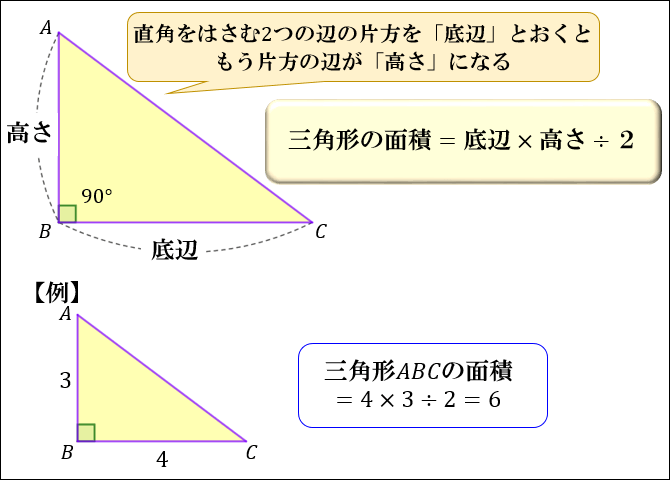
「底辺」を辺 \(BC\) とおくと「底辺 \(BC\) に含まれない頂点 \(A\) から底辺 \(BC\) におろした垂線」は辺 \(AB\) と一致するので、「高さ」は辺 \(AB\) となる。
三平方の定理
直角三角形において、「直角」をはさむ2つの辺の長さを \(a,b\)、斜辺の長さを \(c\) としたとき
\(a×a+b×b=c×c\)
が成り立つことが分かっています。
これを、三平方の定理(別名:ピタゴラスの定理)と言います。

実際に、高さ \(3cm\),底辺 \(4cm\) の直角三角形を描いてみてください。
斜辺の長さがちょうど \(5cm\) になるのが分かるはずです。
直角三角形の斜辺の長さの求め方
三平方の定理を使うと
● 「底辺」と「高さ」から「斜辺の長さ」を求める
● 高さがわからない三角形の面積を求める
● 直角な頂点から斜辺におろした垂線の長さを求める
といったことが可能になります。
①斜辺の長さを求め方
【問①】下図の直角三角形の斜辺の長さ \(c\) を求めてください。
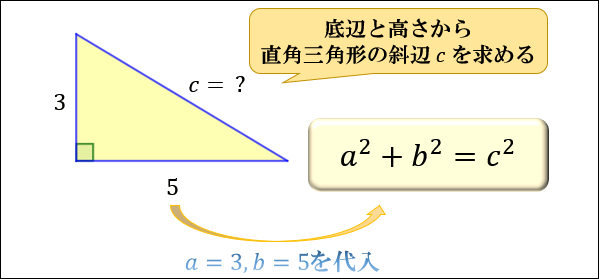
\(a=3,b=5\) を代入すると
\(3×3+5×5=c^2\)
⇔ \(9+25=c^2\)
⇔ \(34=c^2\)
⇔ \(c=\sqrt{34}≒5.831\) となります。
\(\sqrt{34}\) は、\(34\) の正の平方根。二乗したら \(34\) になる正の数のこと。
\(\sqrt{34}×\sqrt{34}=34\)
②高さがわからない直角三角形の面積の求め方
【問②】下図の直角三角形の面積 \(S\) を求めてください。

まず、底辺と斜辺から「高さ \(a\) 」を求めます。
三平方の定理に \(b=3,c=4\) を代入すると
\(a^2+3×3=4×4\)
⇔ \(a^2+9=16\)
⇔ \(a^2=7\)
⇔ \(a=\sqrt{7}≒2.646\) となります。
これを、三角形の面積の公式\(「底辺×高さ÷2」\)に代入すると
\(S=3×\sqrt{7}÷2=\dfrac{3\sqrt{7}}{2}\) となります。
③直角な頂点から斜辺におろした垂線の長さの求め方
【問③】底辺 \(8\)、高さ \(4\) の直角三角形がある。
この直角三角形の直角な頂点から斜辺におろした垂線の長さ \(h\) を求めてください。
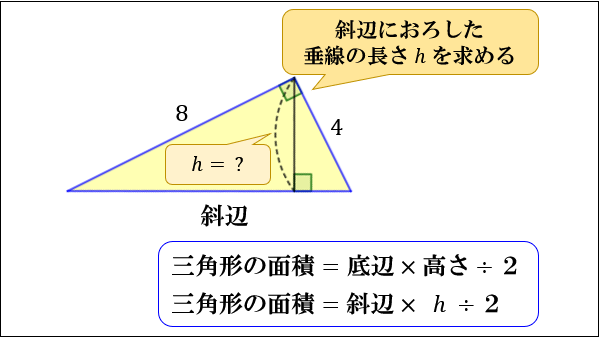
斜辺の長さを \(c\) とおくと
三平方の定理 \(a^2+b^2=c^2\) から
\(8×8+4×4=c^2\)
⇔ \(64+16=c^2\)
⇔ \(80=c^2\)
⇔ \(c=4\sqrt{5}\)
この三角形の面積は
\(8×4÷2=16\)
三角形の面積は\(「斜辺×h÷2」\)でも求まるので
\(4\sqrt{5}×h÷2=16\)
⇔ \(h=\dfrac{8\sqrt{5}}{5}\)
となります。
直角三角形の合同条件とその証明

直角三角形は、上述の(1),(2),(3)の三角形の合同条件以外にも①,②の条件でも合同であることを証明できます。
①斜辺と1つの鋭角がそれぞれ等しい
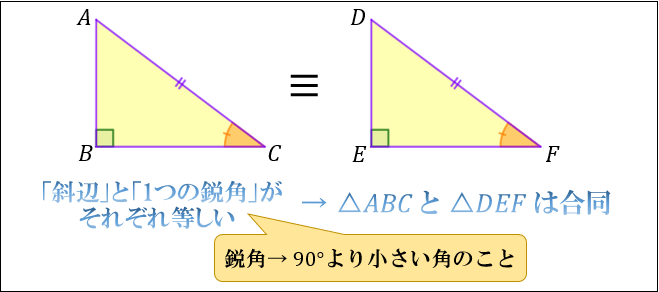
上図の場合、
「斜辺 \(AC=DF\) 」
「1つの鋭角 \(∠C=∠F\) 」
から
\(△ABC≡△DEF\) となります。
【証明】三角形の内角の和は \(180°\) で一定なので
\(∠B=∠E\) かつ \(∠C=∠F\) より、\(∠A=∠D\) となって
斜辺 \(AC=DF\),\(∠A=∠D\),\(∠C=∠F\) で
三角形の合同条件「 (1) 1組の辺とその両端の角が等しい」を満たすため
②斜辺と他の1辺がそれぞれ等しい
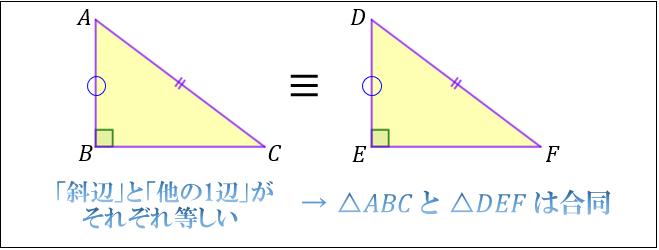
上図の場合、
「斜辺 \(AC=DF\) 」
「他の1辺 \(AB=DE\) 」
から
\(△ABC≡△DEF\) となります。
【証明】三平方の定理から
\(BC^2=AC^2-AB^2\) \(=DF^2-DE^2=EF^2\)
⇔ \(BC=EF\) となり
三角形の合同条件「 (3) 3組の辺がそれぞれ等しい」を満たすため