このページでは、色々な置換積分のやり方を見ていきます。
累乗の中身を \(t\) をおくパターン
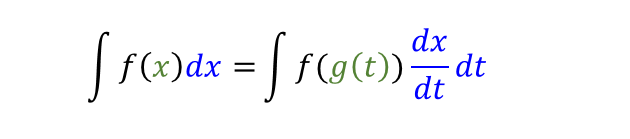
一番基本的なパターン。
累乗の中身を \(t\) とおいてから \(dx/dt\) を求め、変換していきます。

\(g'(x)\) を探すパターン

ルートや累乗といった複雑なかたまりの中身 \(g(x)\) に注目して、それを微分した \(g'(x)\) がどこかに無いか探すパターン。
\(g'(x)\) が見つかれば \(t=g(x)\) とおくことで \(g'(x)dx=\dfrac{dt}{dx}{dx}=dt\) となり、積分しやすい形に変換できます。

\(x=a\sin{θ}\) とおくパターン
\(\sqrt{a^2-x^2}\) の形のパターン
\(\sqrt{a^2-a^2\sin^2{θ}}=\sqrt{a^2\cos^2{θ}}=|a\cos{θ}|\)
と変形するために \(x=a\sin{θ}\) とおくのがコツ。

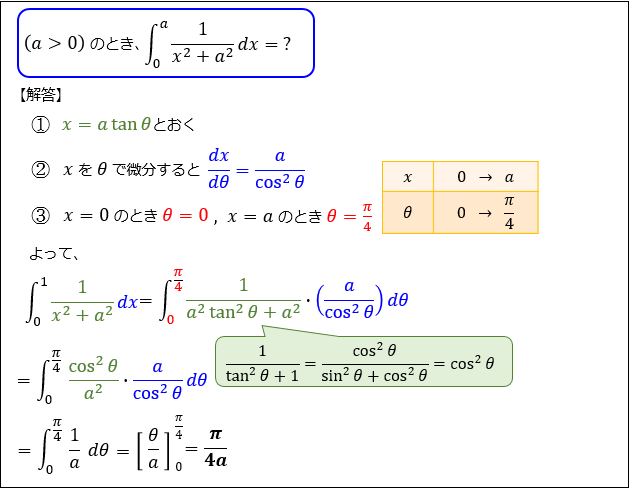
\(x=a\tan{θ}\) とおくパターン
\(\dfrac{1}{x^2+a^2}\) の形のパターン
\(\dfrac{1}{a^2(\tan^2{θ}+1)}=\dfrac{1}{a^2}\cos^2{θ}\)
と変形するために \(x=a\tan{θ}\) とおくと上手くいきます。
>>関連記事:微分の公式一覧
>>関連記事:三角関数の公式一覧

置換積分法とは。5つのステップから分かる置換積分のやり方とコツ 置換積分法とは、変数をうまく変換することで計算量を減らすテクニックです。 たとえば、$\displaystyle \int...