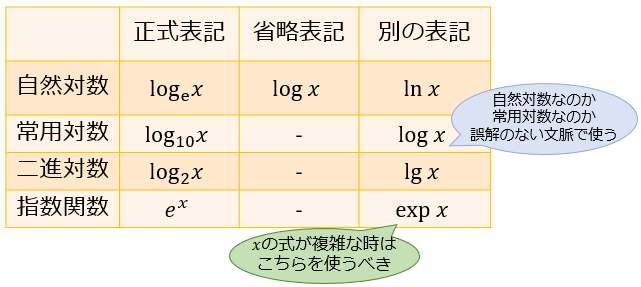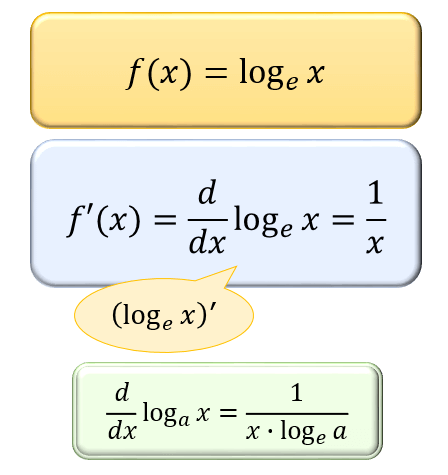
ネイピア数 \(e≒2.718\) に対して、
対数関数 \(f(x)=\log_{e}x\) を \(x\) で微分すると、導関数 \(f'(x)=1/x\) が求まります。
対数関数の微分は、様々な分野において「複雑な微分計算をカンタンに解くための強力なテクニック」として重宝されている重要な単元です。
今回は、そんな対数関数の微分公式の証明方法を解説していきます。
導関数の定義式とその意味
導関数は「曲線 \(y=f(x)\) 上の任意の点 \((x,f(x))\) における接線の傾きを \(x\) の関数として表したもの」に対応する関数で、 \(\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\) で表わされます。
導関数を求めることを「微分する」と言います。
接線の傾きは、同じ曲線上の限りなく近い位置にある2点 \((x,f(x))\)と\((x+h,f(x+h))\) を結ぶ直線の傾き \(\displaystyle \frac{f(x+h)-f(x)}{(x+h)-x} (h\to 0)\) に一致します。

こう考えると、導関数の定義式
\(\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\) の意味も理解しやすいのではないでしょうか。
導関数の定義式から公式を証明してみよう
この定義式から、対数関数の微分公式を証明してみましょう。
導関数の定義式に \(f(x)=\log_{e}x\) を代入し、対数の公式を使うと…
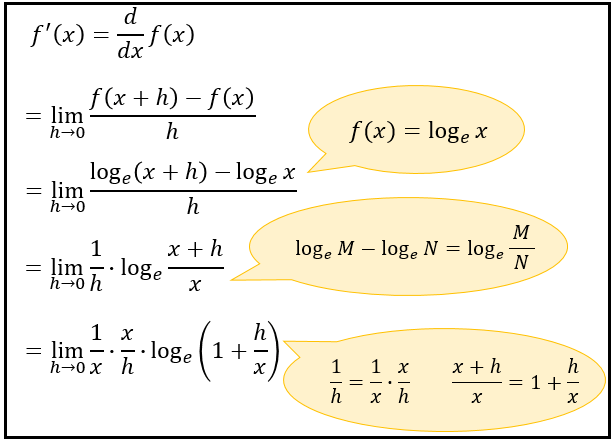
上のような式に変形できます。
ここで、\(\displaystyle \frac{h}{x}=t\) と置くと
\(\displaystyle \frac{x}{h}=\frac{1}{t}\) になるので、ネイピア数の定義式から…
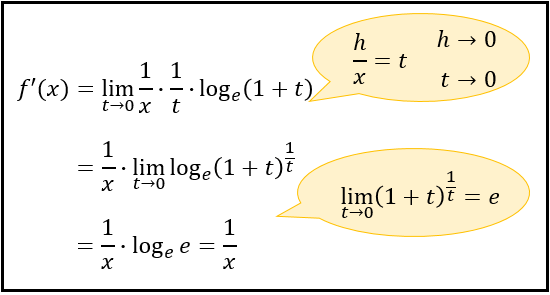
見事、対数関数 \(f(x)=\log_{e}x\) の導関数が \(f'(x)=1/x\) であることを証明できました。
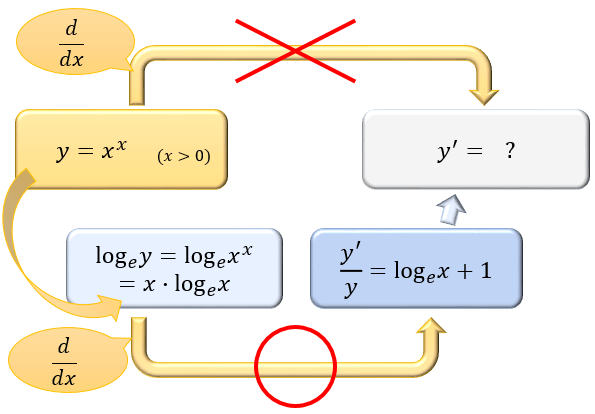
対数微分で便利なこと
対数関数の微分は、
①その導関数が \(1/x\) というシンプルな形で表せる
②真数のかけ算が対数の足し算、真数の累乗が対数のかけ算になる
という性質から、様々な分野において重宝されている強力なテクニックです。
例えば、何らかの確率法則に従って「誤差・ばらつき」が生じていると考えられる事柄に対して、現在までに得られた情報から、どのような推定をするのが「もっともらしい」かを計算する手法である最尤推定法においても、対数微分法という形で利用されています。
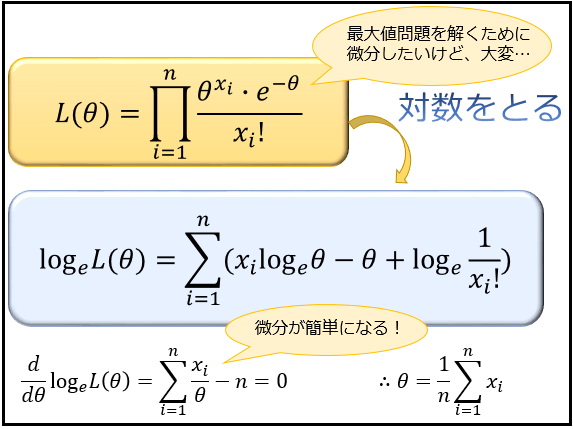
データ分析を行う統計学や、人工知能の領域で「人間が無意識のうちに行っている学習能力と同様の機能」を実現するための研究分野である機械学習などで欠かせない手法なので、この辺りに興味のある方はぜひマスターしておきたいところですね。