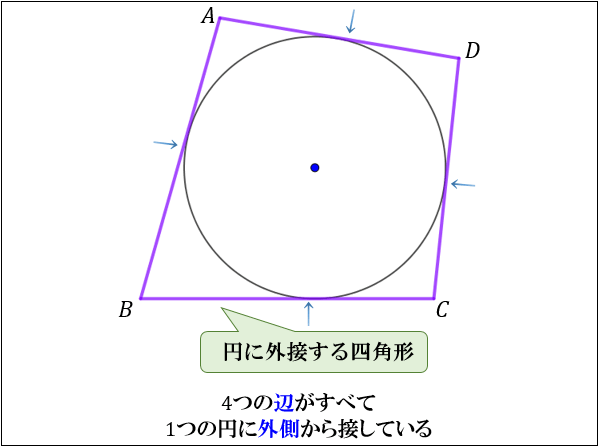
四角形 \(ABCD\) の\(4\)つの辺がすべて同じ円に外側から接しているとき、「四角形 \(ABCD\) は円に外接する」といいます。
>>関連記事:円に内接する四角形の性質まとめ
このページでは、「円に外接する四角形がもつ性質」をみていきましょう。
①1つの頂点から円に向かって引いた2本の接線の長さは等しい
円に外接する四角形 \(ABCD\) について、\(AD,AB\) 上の円の接点をそれぞれ \(P,Q\) とすると、\(AP=AQ\) が成り立つ。
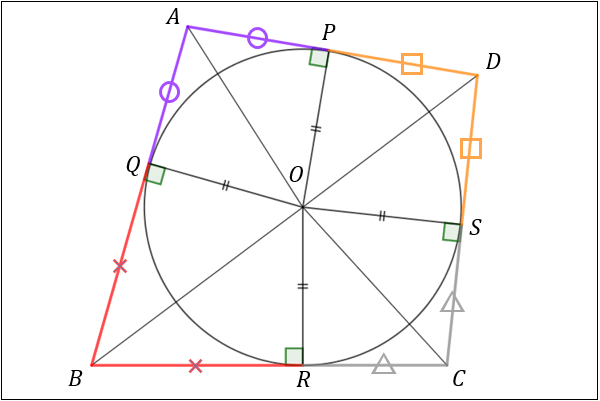
【証明】
点 \(P,Q\) は円の接点なので、\(∠APO=∠AQO=90°\)
よって三角形 \(APO,AQO\) は直角三角形であることから、三平方の定理が成り立ちます。
円の半径 \(OP=OQ=r\) とすると、三平方の定理の式は
\(AO^2=AP^2+OP^2=AP^2+r^2\)
\(AO^2=AQ^2+OQ^2=AQ^2+r^2\)
で表されます。
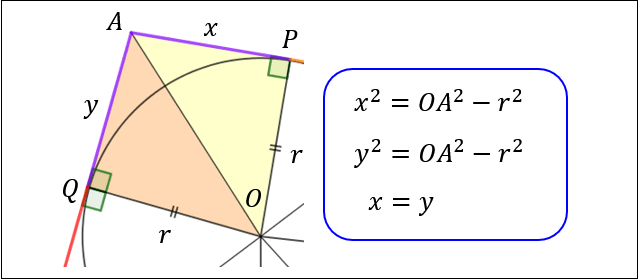
よって、\(AP^2=AO^2-r^2=(AQ^2+r^2)-r^2=AQ^2\) となり
\(AP=AQ\) であることが分かります。
②2組の「向かい合った辺の合計」は等しい
円に外接する四角形 \(ABCD\) について、\(AB+CD=BC+AD\) が成り立つ。

【証明】
先述の「①1つの頂点から円に向かって引いた2本の接線の長さは等しい」から
\(AP=AQ=○\)
\(BQ=BR=×\)
\(CR=CS=\triangle\)
\(DS=DP=□\)
とおくと
\(AB+CD=AQ+BQ+CS+DS\)
\(=○+×+\triangle+□\)
\(BC+AD=BR+CR+DP+AP\)
\(=○+×+\triangle+□\)
となり、\(AB+CD=BC+AD\) を示せました。
③円に外接する四角形の面積の公式
円に外接する四角形 \(ABCD\) の\(4\)辺を \(a,b,c,d\) 、\(∠BAD=θ_1,∠BCD=θ_2\) とおくと
この四角形の面積は \(S=\sqrt{abcd}\sin{\dfrac{θ_1+θ_2}{2}}\) で表される。
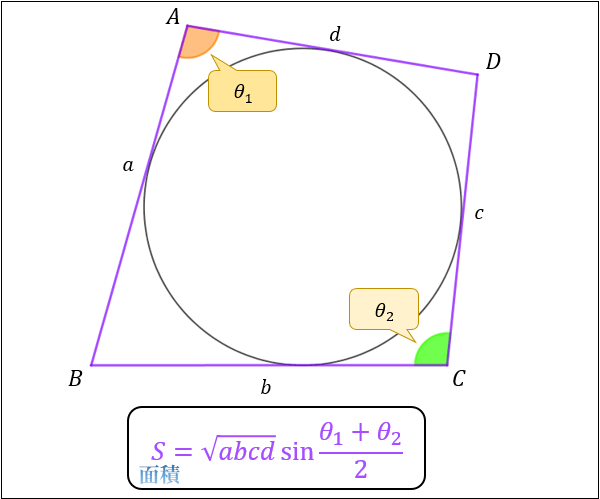
\(\sin{θ}=\sin{180°-θ}\) なので、対角の和であればどちらの対角を使っても構いません。
\(S=\sqrt{abcd}\sin{\dfrac{∠ABC+∠ADC}{2}}\) からも同じ答えが求められます。