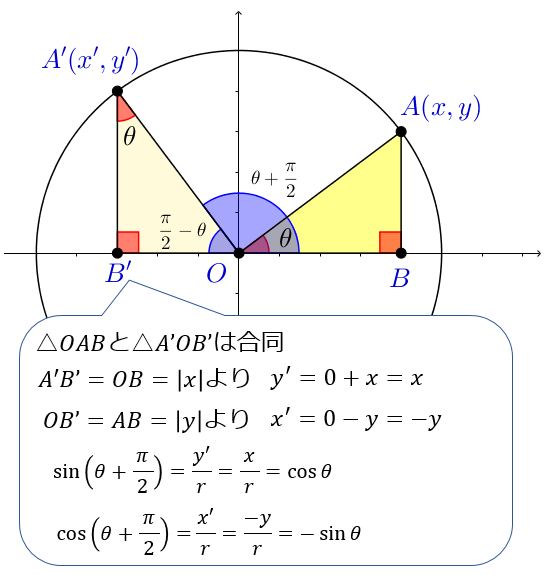今回は、三角関数の基礎知識をできるだけ分かりやすくまとめてみました。
サイン・コサイン・タンジェント
まず、原点 \(O\) を中心とする半径 \(r\) の円と、その円上の点 \(A(x,y)\) を考えます。
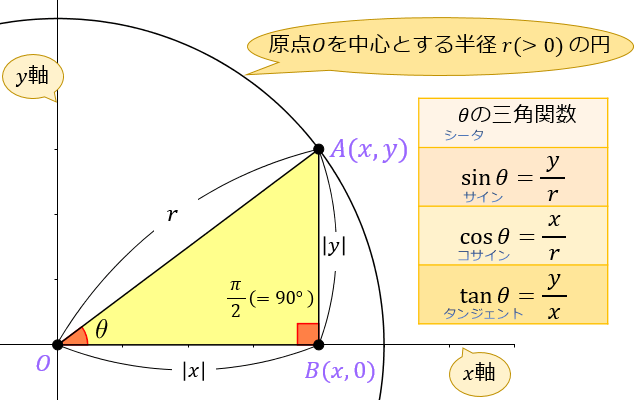
「\(x\) 軸の正の部分」と線分 \(OA\) による(反時計回りを正とする)角の大きさ \(∠BOA=θ\) に対して
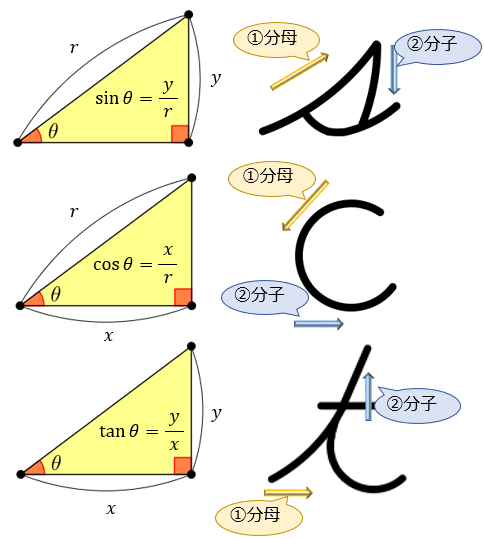
\(\sin{θ} =\dfrac{y}{r}\) \(,\cos{θ}=\dfrac{x}{r}\) \(, \tan{θ} =\dfrac{y}{x}\)
で表される3つの三角比の関数のことを、三角関数と言います。
「\(\sin{θ},\cos{θ},\tan{θ}\) の分母・分子をド忘れしそう…」と感じる方も多いかもしれませんが、これらはその頭文字 s,c,t の筆記体のイメージと結びつけると覚えやすくなりますよ。
弧度法とは?
\(\sin{θ}\) と書くときの \(θ\) は「\(30°,60°\)」といった度数法ではなく、「\(π/6,π/3\)」といった弧度法で表されることが多いです。
弧度法とは「円の半径に等しい長さの弧の中心に対する角度」を \(1\) rad(ラジアン)と定義する計量法のこと。
これは「半径 \(1\) mの円の円弧の長さが \(θ\) mとなるような角度の大きさを \(θ\) radと呼ぶ」と覚えておくと分かりやすくなります。

半径 \(1\) の円の円周は \(2π\) なので、「度数法における \(360°\)」=「弧度法における \(2π\)」となります。
反対に「弧度法における \(1\) 」=「度数法における \(180°/π≒57.3°\)」とも言えますね。

※ \(π\) は円周率\(≒3.14\)

三角比の表
三角比の中でも、\(\sin{θ} ,\cos{θ}\) \((θ=0,π/6\)\(,π/4,π/3,π/2)\) の値はよく使うので、できれば完璧に暗記しておきたいところ。
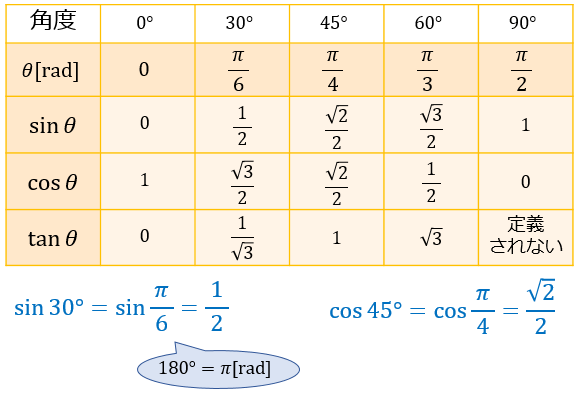
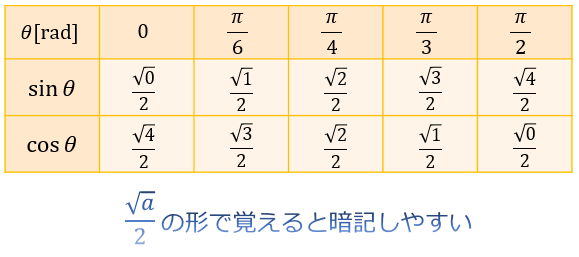
\(\sin{θ}\) と \(\cos{θ}\) は \(\dfrac{\sqrt{a}}{2}\) の形で覚えると暗記しやすいですよ。
\(2π/3≦θ≦2π\) における三角比も見ていくと、こんな感じ。
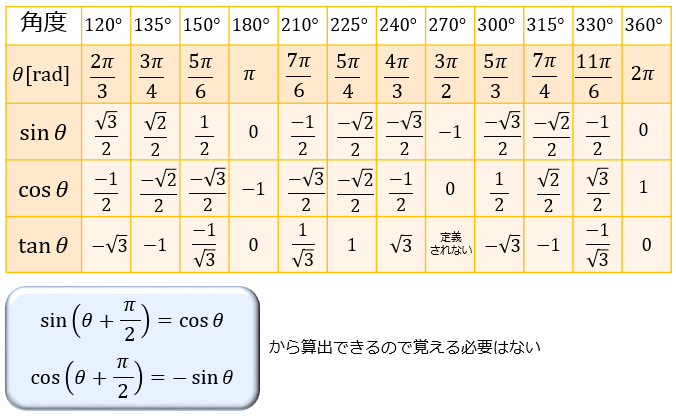
こちらは 「\(θ=0,π/6,π/4,π/3,π/2\)」 の表を覚えておけば後述の公式から求められるので、絶対に暗記しないといけないわけではありません。
三角関数で基本となる4つの式
最後に、三角関数の公式の中でも特によく使う4つの式を紹介します。

1つ目は \(\tan{θ}=\sin{θ} / \cos{θ}\) 。
これは、\(\sin{θ} ,\cos{θ} ,\tan{θ}\) の定義式から求められます。
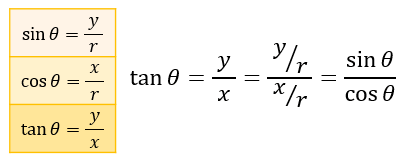
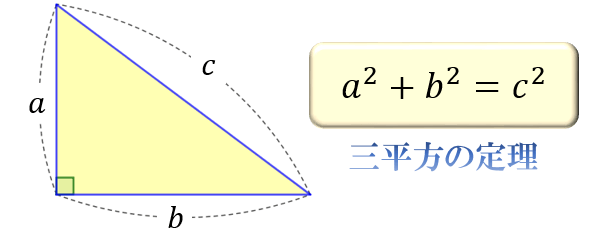
2つ目は \(\sin^2{θ}+\cos^2{θ}=1\) 。
これは、三平方の定理から求められます。


3つ目は \(\tan^2{θ}+1=1/\cos^2{θ}\) 。
これは、先ほどの \(\sin^2{θ}+\cos^2{θ}=1\) の両辺を \(\cos^2{θ}\) で割ってから \(\tan{θ}=\sin{θ} / \cos{θ}\) を当てはめることで求まります。
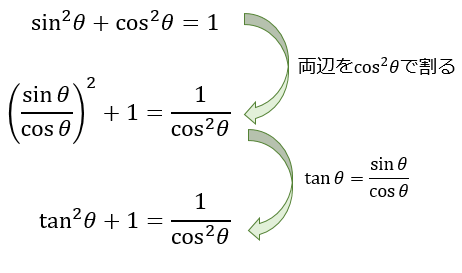
\(cos{θ}\) から直接 \(\tan{θ}\) を求めたいときに便利な公式ですね。
4つ目は \(\sin(θ+π/2)\)\(,\cos(θ+π/2)\) の公式。
これは、さきほどの点 \(A\) を \(π/2 \ (=90°)\) 回転させた点 \(A’\) を考えると分かりやすいです。