「整数の計算」は買い物などでよく使いますが、「分数の計算」は意識していないとあまり使わないものですよね。
「分数の計算って苦手。なぜ勉強するのか分からない」という人も多いのではないでしょうか。
実は分数の計算には、「確率を計算する」という大きな役割があります。
確率を計算できれば、大きな決断をしないといけないときに「どちらの選択をえらんだ方が良いのか」が一気に分かりやすくなるんです。
損をする可能性もグッと低くなってくるでしょう。
分数の計算は、小学生・中学生がつまずきやすいポイントであると同時に、一度キチンと理解すれば一生使い続けられる武器となってくれます。
「苦手だし面倒だからイイや」と思わずに、ここで身につけておきましょう。
photo credit:Bobo Boom
分子と分母
分数は、分子と分母から成り立っています。
横棒の上の数字を「分子」と言い、横棒の下の数字を「分母」と言います。
どちらが「分子」かを忘れてしまったときは、「子供をかかえ上げた母親」をイメージすると思い出しやすくなりますよ。

分数の足し算
分数の足し算は
①:2つの分数の「分母」が同じになるようにそろえて(通分して)から
②:2つの分数の「分子」を足し算をして
③:最後に「約分」をする。
この3つのステップをふむのがコツです。
ここでは、「2/3 + 1/12」を計算してみましょう。
まず、2つの分数の分母「3」と「12」をそろえるために、「2/3」の分子と分母にそれぞれ4をかけます。
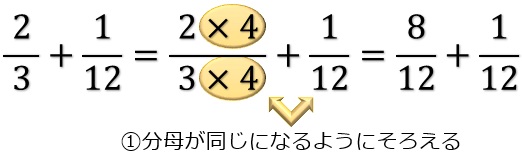
分母をそろえた後は分子どうしを足して、約分するために分子と分母をそれぞれ3で割ります。
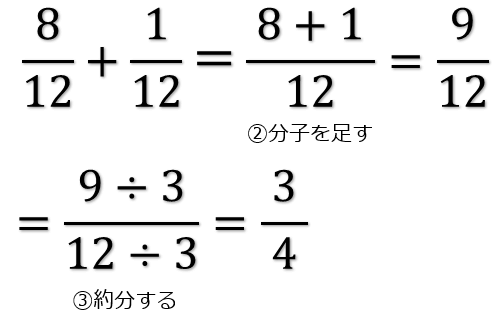
これで「2/3 + 1/12=3/4」が求まりました。
分数の引き算
分数の引き算も
①:2つの分数の「分母」が同じになるようにそろえて(通分して)から
②:2つの分数の「分子」で引き算をして
③:最後に「約分」をする
という3つのステップをふむことで求まります。
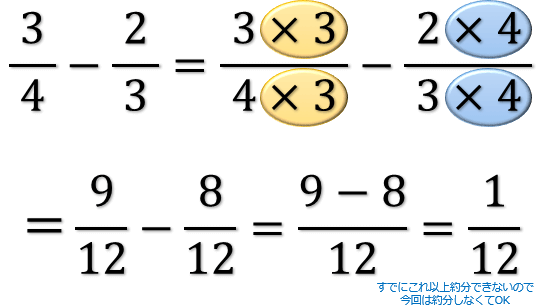
分数の掛け算
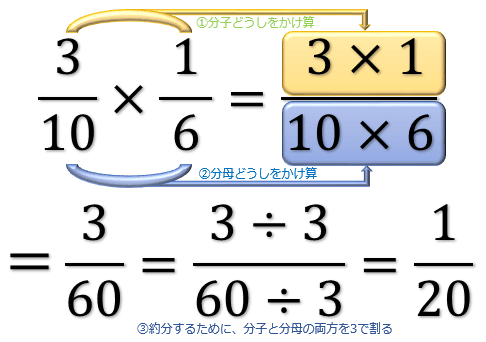
分数のかけ算は
①:分子どうしをかけ算する
②:分母どうしをかけ算する
③:最後に「約分」する
という3つのステップをふむことで求まります。
分数の割り算
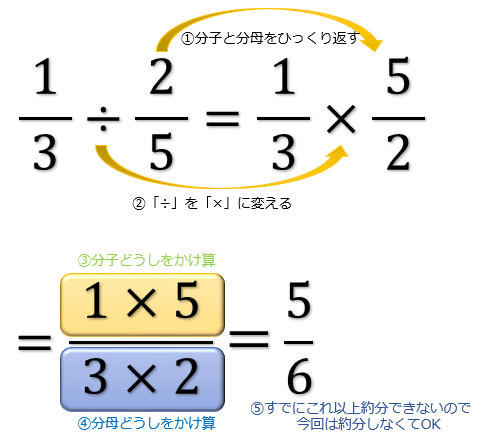
分数の割り算は
①:割る数の分子と分母をひっくり返す
②:「÷」を「×」に変える
③:分子どうしをかけ算する
④:分母どうしをかけ算する
⑤:最後に「約分」する
という5つのステップをふむことで求まります。
ややこしいと思うかもしれませんが、③~⑤は分数のかけ算と同じなので、分数のかけ算問題をたくさん解いてから挑戦してみましょう。
次のページでは「なぜ分数の割り算はひっくり返してかけ算するのか?」を解説していきます。