
今回は、「分散の定義と求め方」・「分散と標準偏差の関係性」・「分散独自の利点」について書いていきます。
photo credit:skyseeker
分散とは何か?その定義
分散とは「データのばらつきの大きさ」を表わす指標で、V[X] または σ2 または s2 で表わされる数値です。
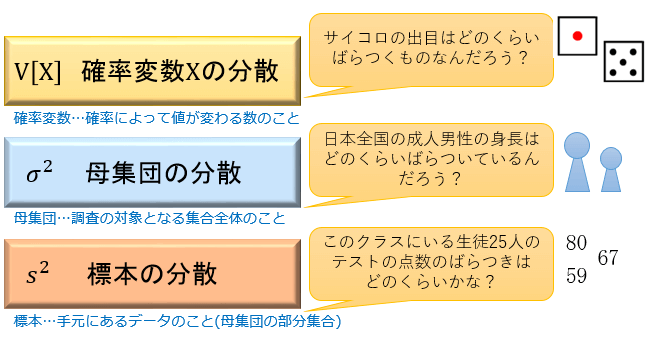
分散は「確率変数Xからその母平均を引いた変数の2乗の期待値」として定義されます。
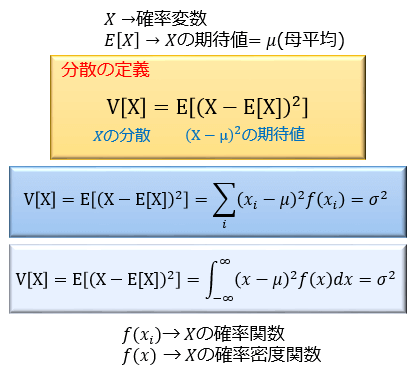
とりあえずは「平均との差を2乗した値の期待値」を分散と呼ぶ、とおさえておくと分かりやすいかなと思います。
実際に分散を求めてみよう
標本の分散(手元にあるデータのばらつきの大きさ)を求める場合、先ほどの定義式は「各データの値と平均の差の2乗の合計を、データの総数で割った値」という公式に変形できます。
まずは、実際にこの公式を使って標本の分散を求めてみましょう。
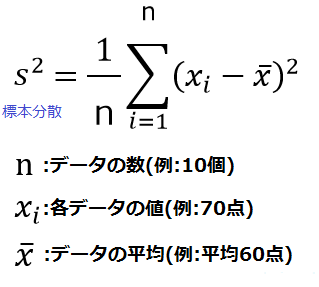
たとえば、5人の英語・数学・歴史のテストの点数が以下のようになっていたとします。
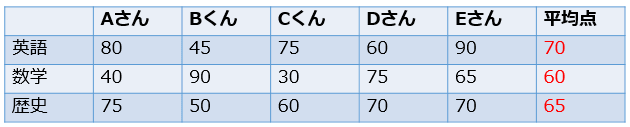
データの数はそれぞれ5個なので、n=5
これを、先ほどの公式に当てはめていくと…
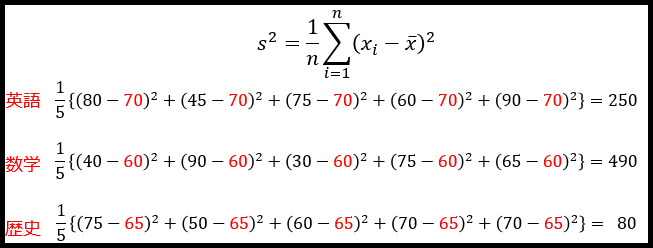
「英語の分散が250」「数学の分散が490」「歴史の分散が80」と求まりました。
ここから、「歴史が一番点数のばらつきが小さいテストで、数学が一番点数のばらつきが大きいテストだった」という事が判断できます。
分散と標準偏差の違い
ばらつきの大きさを表す指標としては、「分散」の他にも「標準偏差」が存在します。
この2つは非常によく似ていて、「分散の正の平方根が標準偏差」↔「標準偏差の2乗が分散」という関係にあります。
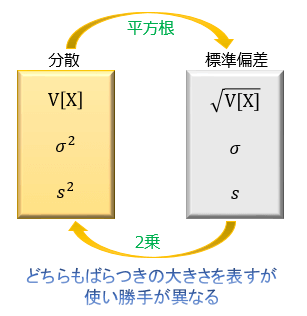
どちらも「データのばらつきの大きさ」を表すという意味ではほとんど差がありませんが、分散には分散の良さがあり、標準偏差には標準偏差の良さがあるので、状況に応じて2つを使い分けることが重要になってきます。
例えば、標準偏差は「元のデータの数値と単位がそろっている」おかげで、正規分布を仮定した場合に「68%95%ルール」が存在し、これがデータ分析をする上で便利だということは標準偏差の記事で書いたとおり。
分散独自の利点
では、標準偏差にはない分散独自の利点は何なのか?
その答えとしては、平方根を使っていないおかげで「関数表記で扱いやすい」「不偏推定量の計算が楽」などが挙げられます。
関数表記で扱いやすい
分散は平方根を使っていないため、関数表記で扱いやすいという特徴があります。

これは、数式的にややこしくなりやすい「平方根」を使う標準偏差にはない利点です。
不偏分散は不偏標準偏差より計算が楽
推測統計学においては、「不偏推定量」という値を求めることが重要になってきます。
ただ、母分散の不偏推定量である不偏分散は、標本分散をn/(n-1)倍した値なのに対し
母標準偏差の不偏推定量である不偏標準偏差(母集団が正規分布の場合)は、ガンマ関数というややこしい関数が絡んできて数式的に扱いにくくなってしまうという特徴があります。
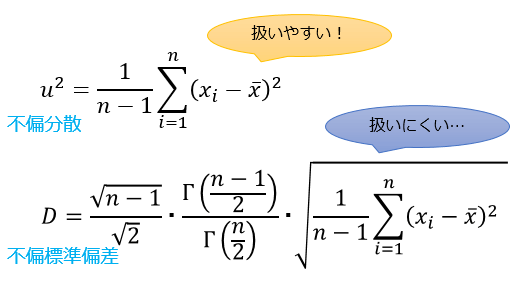
パッと見ただけでも、不偏標準偏差の扱いにくさが伝わってきますよね。
区間推定や検定においても『不偏標準偏差 D 』ではなく、『不偏分散による標準偏差 u (不偏分散の平方根)』が使われるのも、これが原因と考えられます。(※ t 分布と相性が良い)
「標準偏差の方が、実際に数字を代入した時に直感的に理解しやすい」
とおさえておけばOKです。





