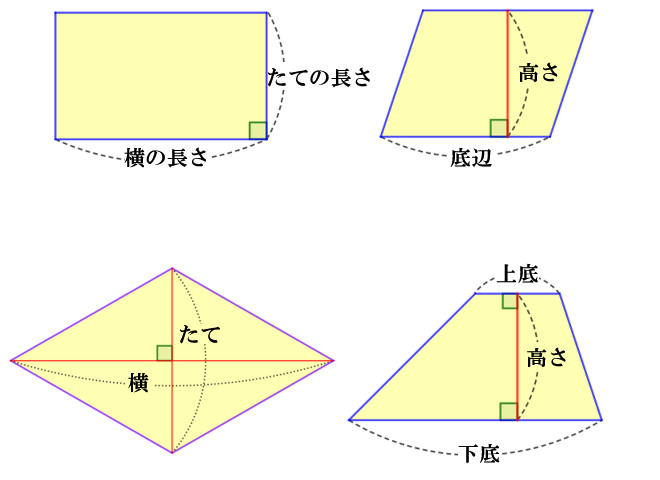
このページでは、円周の長さと円の面積の求め方について解説していきます。
円周の長さの求め方
円のまわりの長さを求めるときは
円周の長さ \(=\) 直径 \(×\) 円周率
という公式を使います。

半径とは、「円周上の1点」と「円の中心」を結ぶ線の長さのこと。
直径は、半径の2倍。
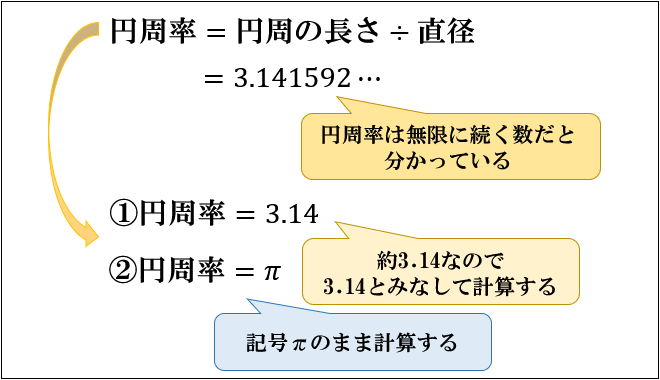
円周率とは「円の直径に対する円周の長さの比」のことで、\(3.1415\cdots\) と無限に続く数であることが分かっています。
無限に続く数をそのまま書くわけにはいかないので、円周率を使うときは
- 円周率の近似値である \(3.14\) とみなして計算する(算数)
- 円周率を記号 \(π\) とおいて、記号のまま計算する(数学)
のどちらかで計算することになります。
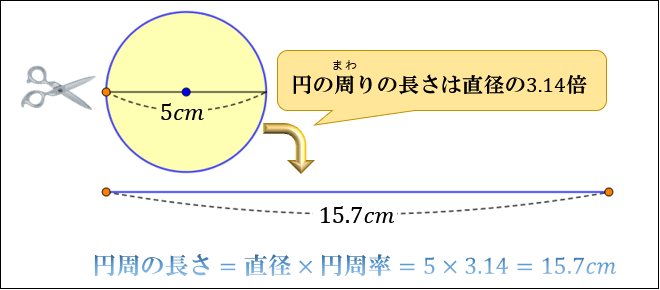
たとえば、直径が \(5cm\) の円のまわりの長さは
\(直径×円周率=5×3.14=15.7cm\)
と求めることができます。
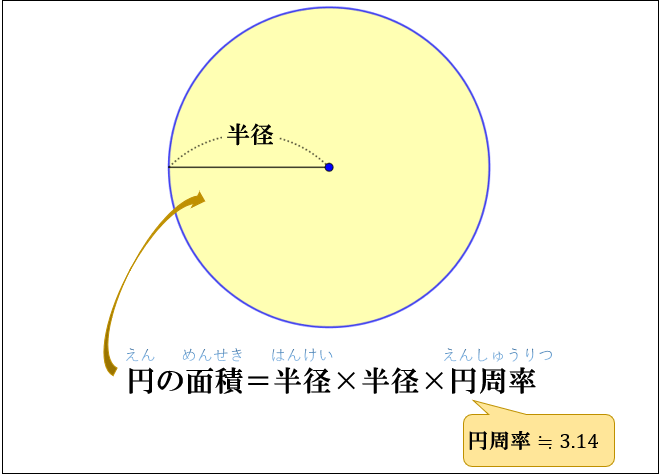
円の面積の求め方
円の面積を求めるときは
円の面積 \(=\) 半径 \(×\) 半径 \(×\) 円周率
という公式を使います。
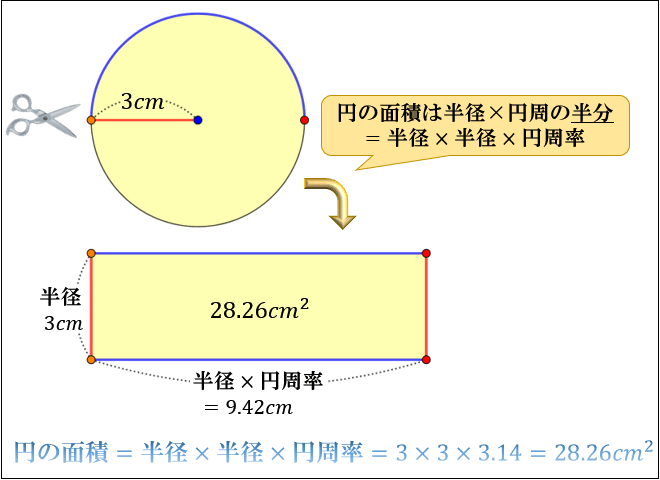
たとえば、半径が \(3cm\) の円の面積は
\(半径×半径×円周率\) \(=3×3×3.14=28.26cm^2\)
と求めることができます。
練習問題
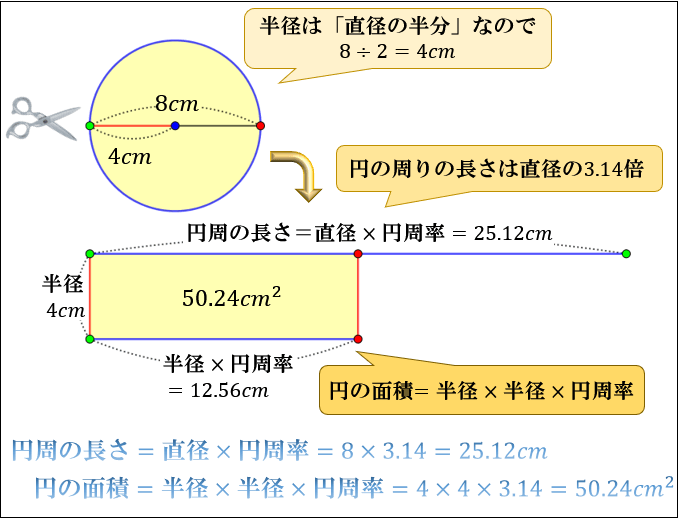
【問①】直径が \(8cm\) の円のまわりの長さと面積を求めてください。(円周率は \(3.14\))
公式に当てはめると
\(円周の長さ=直径×円周率\) \(=8×3.14=25.12cm\)
\(半径=直径÷2=8÷2=4cm\)
\(円の面積=半径×半径×円周率\) \(=4×4×3.14=50.24cm^2\)
と求まります。
【問②】面積が \(153.86cm^2\) の円の円周の長さを求めてください。(円周率は \(3.14\))
円の面積の公式から半径を計算したあと
「半径⇒直径⇒円周の長さ」の順に求めていきます。

公式に当てはめることで、円周の長さが \(43.96cm\) と求まりました。