このページでは、正方形・長方形・平行四辺形・ひし形・台形の面積の求め方とその仕組みについてまとめています。
① 正方形・長方形の面積
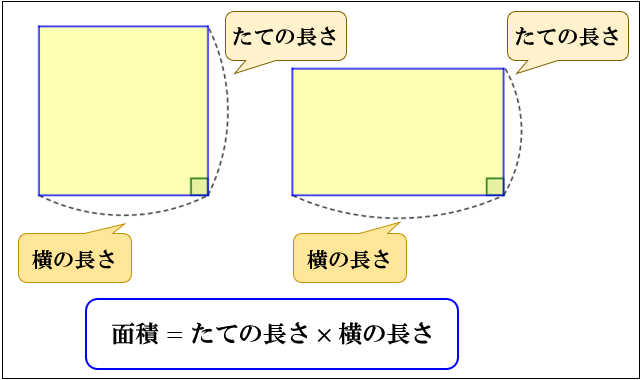
正方形や長方形の面積は、\(「面積=たての長さ×横の長さ」\) で求められます。
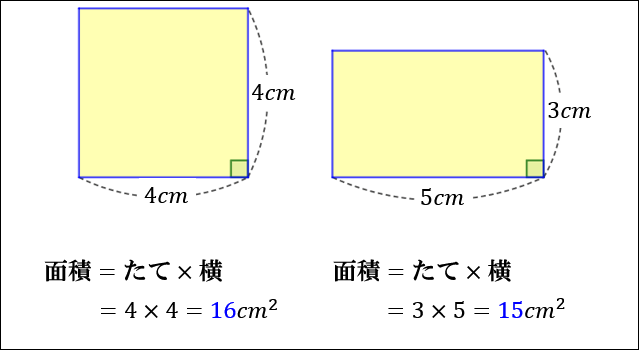
【例題】「1辺の長さ \(4cm\) の正方形」の面積と「たての長さ \(3cm\),横の長さ \(5cm\) の長方形」の面積を求めてください。
「1辺の長さ \(4cm\) の正方形」は、たての長さも横の長さも \(4cm\) なので
\(面積=4×4=16cm^2\)
「たての長さ \(3cm\),横の長さ \(5cm\) の長方形」は
\(面積=3×5=15cm^2\) となります。
② 平行四辺形の面積
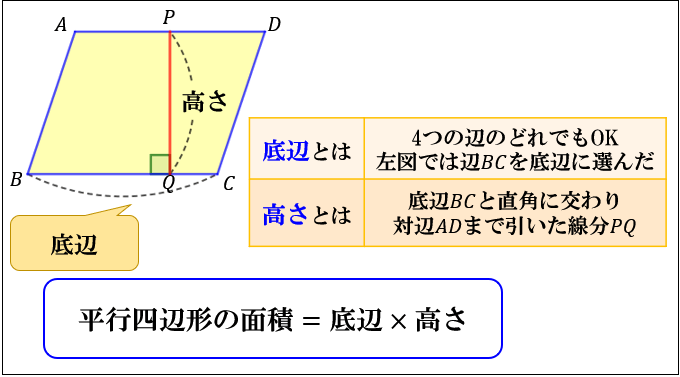
平行四辺形の面積は、\(「面積=底辺×高さ」\) で求められます。
たとえば、「底辺 \(4cm\),高さ \(3cm\) の平行四辺形」の面積は
\(4×3=12cm^2\) となります。
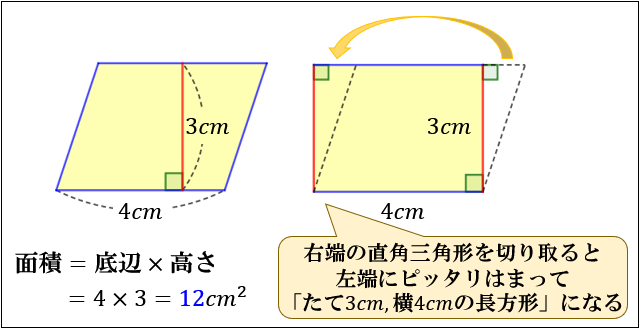
これは、平行四辺形の右端の直角三角形を切り取って左側に移すと
「たて \(3cm\) 横 \(4cm\) の長方形」になるので
\(たて×横=3×4=12cm^2\) からも求められますね。
③ ひし形の面積
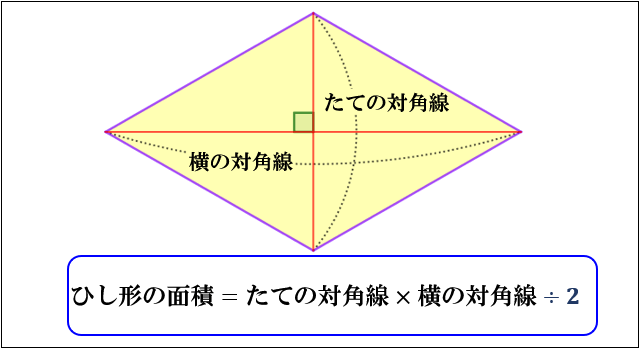
ひし形の面積は、\(「面積=たての対角線×横の対角線÷2」\) で求められます。
たとえば、「2つの対角線の長さが \(4cm\), \(7cm\) の平行四辺形」の面積は
\(4×7÷2=14cm^2\) となります。
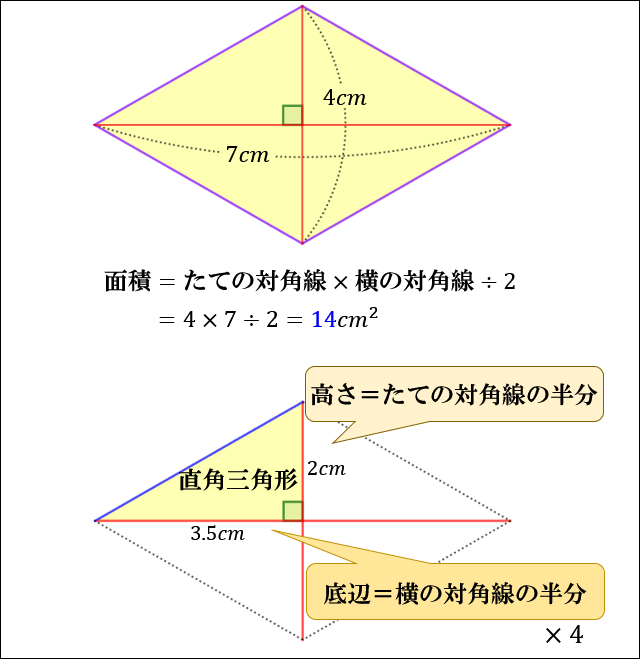
ひし形の面積の公式は「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の4倍と考えると分かりやすいです。
「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の面積は
\(高さ×底辺÷2=(たて÷2)×(横÷2)÷2\)
\(=たて×横÷8\)
となります。
ひし形の面積は、この直角三角形の面積の4倍なので
\(ひし形=直角三角形×4=(たて×横÷8)×4\)
\(=たて×横÷2\)
となり、ひし形の面積の公式が求まります。
④ 台形の面積
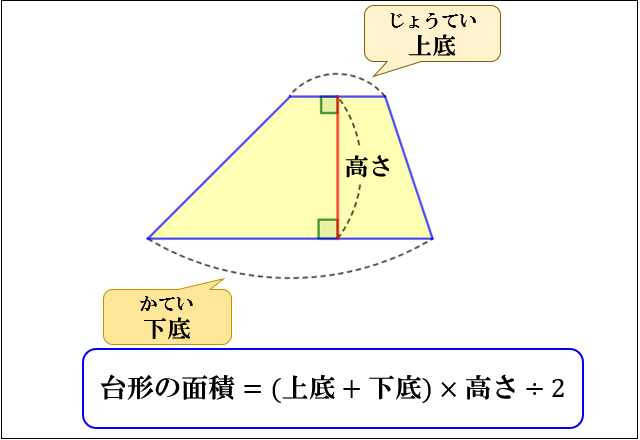
台形の面積は、\(「面積=(上底+下底)×高さ÷2」\) で求められます。
たとえば、「上底 \(2cm\),下底 \(6cm\),高さ \(3cm\) の台形」の面積は
\((2+6)×3÷2=12cm^2\) となります。
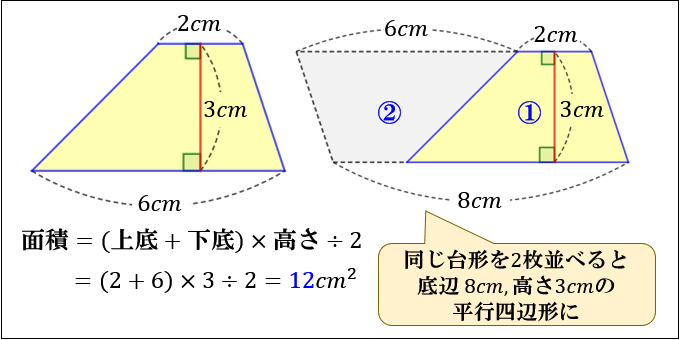
これは、同じ台形を2枚並べると
\(「底辺=上底+下底」「高さ=台形の高さ」\) の平行四辺形になるので
\(台形=平行四辺形の半分=底辺×高さ÷2\)
\(=(上底+下底)×高さ÷2\)
となることからも分かります。
⑤どれにも当てはまらない四角形
以上のどれにも当てはまらない四角形の場合は、ヘロンの公式や三角関数を使った公式からその面積を求められます。
次のページでは、そんな「特殊な四角形」の面積の求め方を見ていきましょう。