2つの三角形が合同であることを示すための条件を、三角形の合同条件と言います。

以下の3つの合同条件のうち、どれか1つでも成り立っているなら「それらの三角形は合同である」ということができます。
条件① 3組の辺がそれぞれ等しい
条件② 2組の辺とその間の角がそれぞれ等しい
条件③ 1組の辺とその両端の角がそれぞれ等しい
条件① 3組の辺がそれぞれ等しい
3組の辺の長さがそれぞれ等しいとき「それらの三角形は合同である」ということができます。
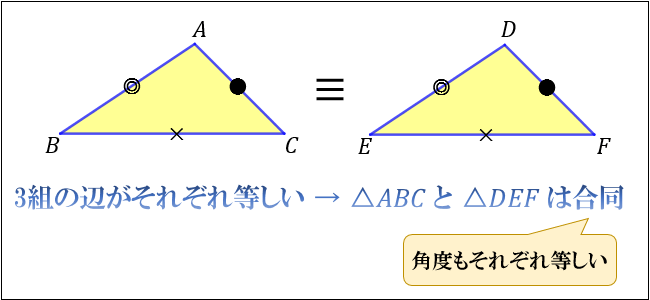
上図の場合、\(AB=DE\)、\(BC=EF\)、\(CA=FD\) で3組の辺の長さがそれぞれ等しいことから、合同となります。
合同であることから、\(∠A=∠D\)、\(∠B=∠E\)、\(∠C=∠F\) であることも分かります。
条件② 2組の辺とその間の角がそれぞれ等しい
2組の辺の長さが等しく、その間の角も等しいとき「それらの三角形は合同である」ということができます。
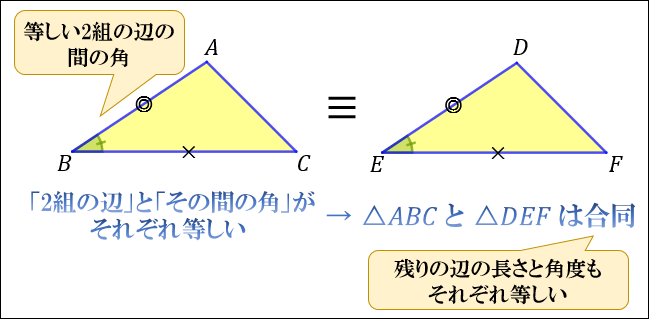
上図の場合、\(AB=DE\)、\(BC=EF\)、\(∠B=∠E\) で2組の辺の長さとその間の角がそれぞれ等しいことから、合同となります。
合同であることから、\(CA=FD\)、\(∠A=∠D\)、\(∠C=∠F\) であることも分かります。
条件③ 1組の辺とその両端の角がそれぞれ等しい
1組の辺の長さと、その両端の角がそれぞれ等しいとき「それらの三角形は合同である」ということができます。

上図の場合、\(BC=EF\)、\(∠B=∠E\)、\(∠C=∠F\) で1組の辺の長さとその両端の角がそれぞれ等しいことから、合同となります。
合同であることから、\(AB=DE\)、\(CA=FD\)、\(∠A=∠D\) であることも分かります。

相似条件と合同条件の違い
最後に、三角形の相似条件と合同条件の比較です。
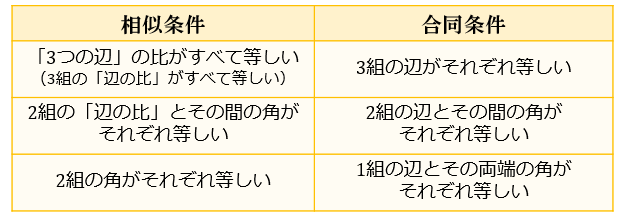
相似条件に加えて、「対応する辺の長さがそれぞれ等しい」という条件が加わることで、合同条件になることがわかります。