
「実数 \(a\) にかけたら \(1\) になる数」のことを逆数といい、\(a^{-1}\) と書きます。

これに対して
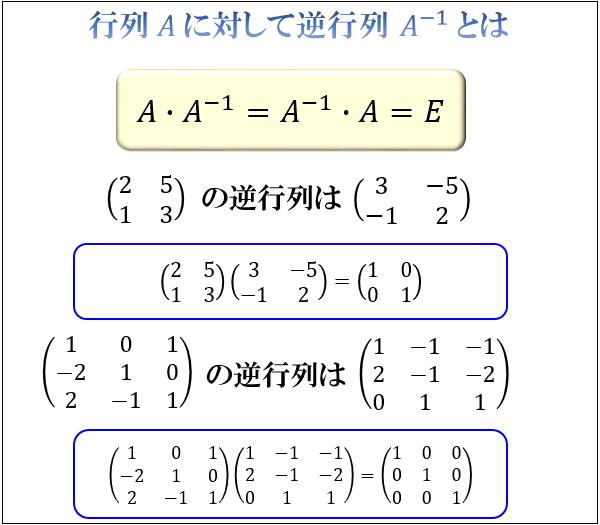
「行列 \(A\) にかけたら単位行列 \(E\) になる行列」のことを逆行列といい、\(A^{-1}\) と書きます。
逆行列は、一言でいうと「逆数の行列バージョン」を意味します。
このページでは、「逆行列・正則行列・特異行列の意味」「逆行列が存在するための条件」「2×2行列の逆行列の公式」を見ていきましょう。
逆行列・正則行列・特異行列とは?
\(n\) 次の正方行列 \(A\) 、単位行列 \(E\) に対して
\(A×A^{-1}=A^{-1}×A=E\)
を満たす行列 \(A^{-1}\) のことを、「\(A\) の逆行列」(Inverse Matrix)と言います。
行列 \(A\) に逆行列が存在するとき、「\(A\) は正則行列である」と言います。
反対に、行列 \(A\) に逆行列が存在しないとき、「\(A\) は特異行列である」と言います。
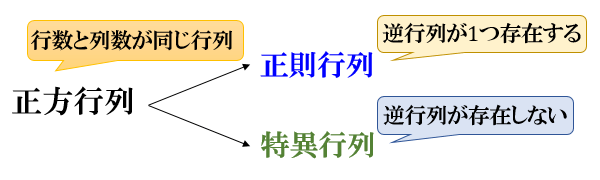
\(A\) が正則行列であるとき、逆行列 \(A^{-1}\) はただ1つ存在します。
1つの行列に2つ以上の逆行列が存在することはありません。
具体例から分かる逆行列と正則行列
たとえば、\(\left(\begin{array}{cc}2 & 5\\1 & 3 \end{array}\right)\) は \(\left(\begin{array}{cc}3 & -5\\-1 & 2 \end{array}\right)\) をかけると単位行列 \(\left(\begin{array}{cc}1 & 0\\0 & 1 \end{array}\right)\) になりますよね。
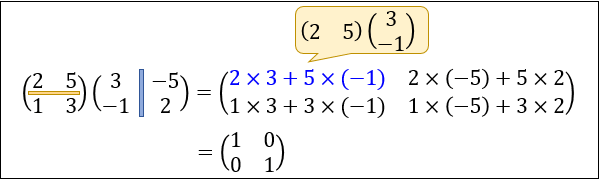
ここから
● \(\left(\begin{array}{cc}3 & -5\\-1 & 2 \end{array}\right)\) は \(\left(\begin{array}{cc}2 & 5\\1 & 3 \end{array}\right)\) の逆行列である
● \(\left(\begin{array}{cc}2 & 5\\1 & 3 \end{array}\right)\) は正則行列である(正則である)
と言うことができます。
一方、\(\left(\begin{array}{cc}2 & -6\\-1 & 3 \end{array}\right)\) にはどんな行列をかけても単位行列 \(\left(\begin{array}{cc}1 & 0\\0 & 1 \end{array}\right)\) にはなりません。
ここから
● \(\left(\begin{array}{cc}2 & -6\\-1 & 3 \end{array}\right)\) には逆行列が存在しない
● \(\left(\begin{array}{cc}2 & -6\\-1 & 3 \end{array}\right)\) は特異行列である(正則でない)
と言うことができます。
逆行列が存在するための条件
行列 \(A\) に逆行列 \(A^{-1}\) が存在するためには、ある条件を満たす必要があります。
その条件とは、「行列式 \(|A|≠0\)」です。

行列式 \(|A|\) を求めることで、その行列に逆行列が存在するかどうかがパッと分かります。
行列積の逆行列
2つの行列の積 \(AB\) の逆行列は
\((AB)^{-1}=B^{-1}A^{-1}\)
で表すことができます。
まとめ
● \(A\) の逆行列とは、「\(A\) にかけたら単位行列 \(E\) になる行列 \(A^{-1}\)」のこと
● \(A×A^{-1}=A^{-1}×A=E\)
● 正則行列とは、「逆行列が存在する行列」のこと
● 正則行列には、逆行列がただ1つ存在する。「逆行列が2つ以上ある行列」は存在しない
● 特異行列とは、「逆行列が存在しない行列」のこと
● 行列式 \(|A|≠0\) のとき、\(A\) は正則行列である(逆行列が1つ存在する)
● 行列式 \(|A|=0\) のとき、\(A\) は特異行列である(逆行列が存在しない)
● \((AB)^{-1}=B^{-1}A^{-1}\)
逆行列の求め方
逆行列の意味が分かったら、次は逆行列の求め方です。
次のページでは、逆行列の求め方を見ていきましょう。



