逆数。英語では”Reciprocal”。
ある数Aに対して、『B=1/A』となるBをAの逆数と言います。
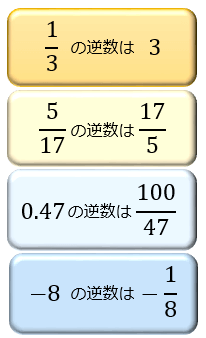
たとえば、5/17 の逆数は 17/5。-8 の逆数は -1/8 となります。
今回は、そんな逆数についてのお話。
photo credit:Always Shooting
逆数の意味と求め方
逆数とは、簡単に言うと「かけたら1になる数」のことです。
たとえば、「Aの逆数」とは『A×B=1』となるような数「B」のことを指します。
「1/3の逆数」→1/3にかけたら1になる数→「3」 (1/3×3=1より)
逆数は、分数の分母と分子をひっくり返すことで、簡単に求めることができます。
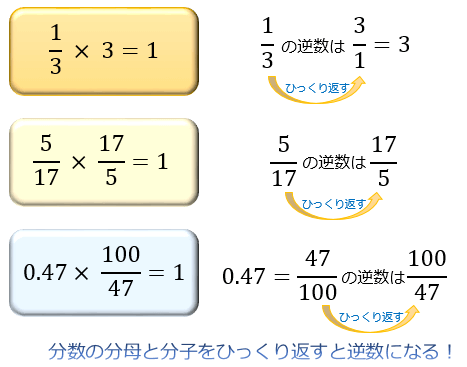
分数ではない数の場合は、まず分数表記に直してからひっくり返せばOKです。
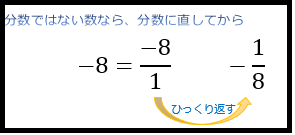
逆数は、例えば分数の割り算を計算するときなどに重宝します。
また、例外的に「0」には逆数が存在しません。
0には何をかけても0になるので、「かけたら1になる数」が存在しないからです。
これが、0で割ってはいけない理由につながっていきます。

自然数の逆数の総和(調和級数)は無限大に発散する
自然数の逆数の総和は、無限大に発散することが分かっています。
自然数の総和(1+2+3+…)が無限大に発散するのは直観的に何となくイメージできると思いますが、どんどん小さい数になっていく「自然数の逆数」の総和も無限大に発散するというのは意外に思われる方も多いのではないでしょうか。
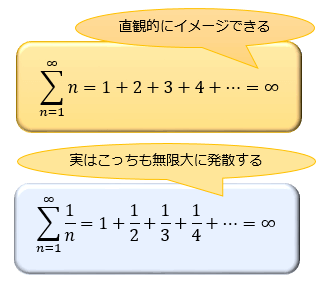
「自然数の逆数の総和」は、一般に調和級数と呼ばれています。
証明方法
調和級数が無限大に発散することは、意外と簡単に証明できます。

上図のように「2のk乗」(4,8,16,32…)ごとにカッコで囲うと、各カッコ内の数の合計がそれぞれ1/2よりも大きいことが分かります。
これにより、調和級数は「1に1/2を無限回足した値よりも大きい」ことが分かるので、調和級数も無限大に発散することが分かります。