
最大公約数とは、2つ以上の正の整数に共通する約数の中で一番大きい数のことを言います。
このページでは、約数の意味から最大公約数の計算方法・カンタンな覚え方を見ていきましょう。
photo credit:April Killingsworth
約数とは
約数とは、ある整数を割り切れる整数(余りが \(0\) になる整数)のことを言います。
たとえば
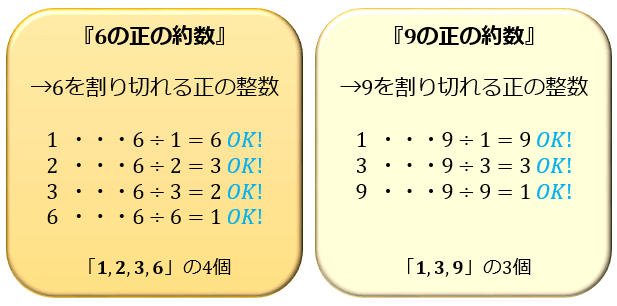
「 \(6\) の正の約数」とは、\(6\) を割り切れる正の整数なので「\(1,2,3,6\)」の \(4\) つ
「 \(9\) の正の約数」とは、\(9\) を割り切れる正の整数なので「\(1,3,9\)」の \(3\) つ
となります。
※正の数とは、0より大きい数のことです。
反対に、\(4\) や \(5\) は「\(6\) の約数」ではありません。
「\(6÷4=1\) あまり \(2\) 」
「\(6÷5=1\) あまり \(1\) 」
のように \(4\) や \(5\) では「\(6\) を割り切れない(余りが \(0\) にならない)」からです。
約数には、「元の数と同じか、それより小さな数」という特徴があります。
つまり、『 \(6\) の約数』は必ず「\(6\) 以下の数」になるんです。
これは『約』という字に「約束・節約といったギュッと絞るイメージ」をつけておくと覚えやすいです。(※約束→小指をギュッと結ぶ。節約→財布のひもをギュッと絞る)
最大公約数の意味と求め方
2つ以上の整数に共通する約数のことを「公約数」と言います。
そして、公約数の中で最大のものを「最大公約数」と言います。
具体的に『 \(24\) と \(36\) の最大公約数』を求め方をみていきます。
Step①2つの数の約数をそれぞれ求めよう!
『 \(24\) と \(36\) の最大公約数』は「 \(24\) と \(36\) に共通する約数の中で一番大きな数」を指します。
そこでまずは、『 \(24\) の正の約数』と『 \(36\) の正の約数』をそれぞれ求めていきましょう。
『 \(24\) の正の約数』とは「\(24\) を割り切れる正の整数」のことなので
\(24÷1=24,24÷2=12 \cdots\) という感じに \(1\) から順番に \(24\) を割っていくことで調べることができます。
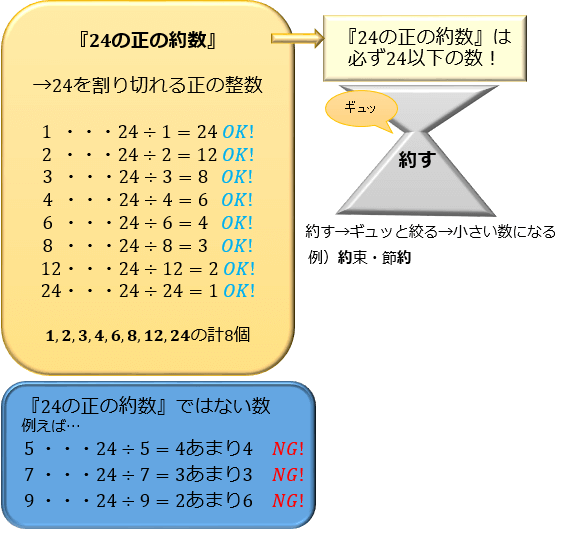
計算してみると、「\(1,2,3,4,6,8,12,24\)」の \(8\) 個が \(24\) を割り切れる数だと分かりますよね。
この「\(1,2,3,4,6,8,12,24\)」の \(8\) 個が、『 \(24\) の正の約数』となります。
次に、\(36\) についても同じように計算してみましょう。
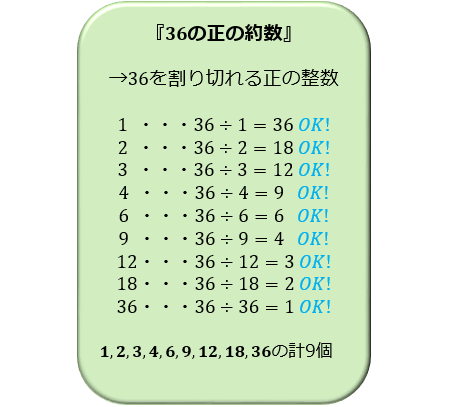
この計算結果から、「\(1,2,3,4,6,9,12,18,36\)」の \(9\) 個が『 \(36\) の正の約数』であることが分かります。
ワンポイントアドバイス
約数を1つずつ求めていると「本当にこれで約数を全部求められたのかな…」と不安になりますよね。
そこで役に立つのが「素因数分解で約数の個数を調べるテクニック」です。
実は素因数分解というテクニックを使うと、約数が全部で何個あるのかが1発で分かるようになるんです。
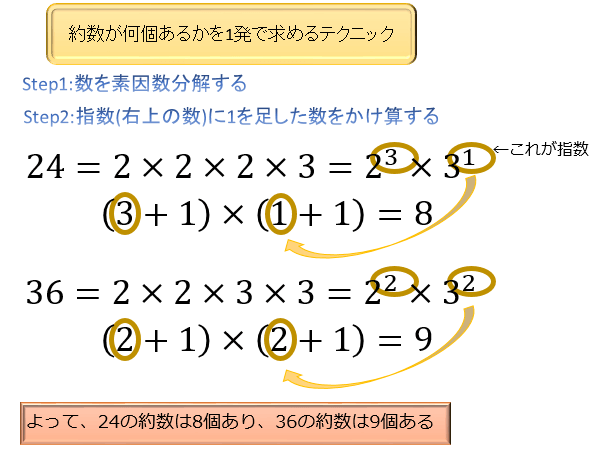
※素因数分解: \(24=2×2×2×3\) といったように、素数のかけ算に分解すること
「素因数分解によると \(24\) の約数は \(8\) 個あるはずなのに、まだ \(7\) 個しか求められていない…。あと \(1\) 個を探してみよう!」と判断できるようになるので、ケアレスミスが少なくなりますよ。
\(210=2×3×5×7\) なら、約数の数は \((1+1)×(1+1)×(1+1)×(1+1)=16\)個
Step②それぞれの約数の中で、共通するものを見つけよう!
『 \(24\) の正の約数』と『 \(36\) の正の約数』を求めたら、今度は『 \(24\) の正の約数』と『 \(36\) の正の約数』の中で共通するものを探してみましょう。
イメージとしては下図のような感じです。
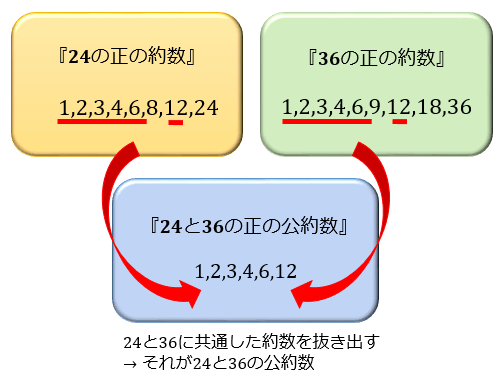
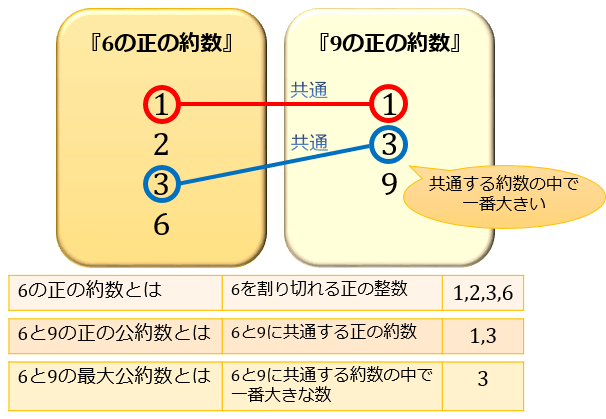
『 \(24\) の正の約数』と『 \(36\) の正の約数』を見比べてみると、「\(1,2,3,4,6,12\)」が共通していますよね。
この6つの数「\(1,2,3,4,6,12\)」が『 \(24\) と \(36\) の正の公約数』となります。
Step③公約数の中で一番大きな数はどれ?
それでは、先ほど求めた『 \(24\) と \(36\) の正の公約数』の中で、一番大きな数はどれでしょうか?
「\(12\)」ですよね。

そして最大公約数とは、公約数の中で一番大きな数のことでした。
よって、この「\(12\)」が『\(24\) と \(36\) の最大公約数』となるわけです。
最大公約数まとめ
①最大公約数とは、公約数の中で一番大きな数のこと。「2つ以上の正の整数に共通する約数の中で一番大きい数」を指す
②約数は、必ず「元の数と同じか、それよりも小さな数」になる。\(24\) の約数は必ず \(24\) 以下であり、\(36\) の約数は必ず \(36\) 以下
③これは、『約』という字に「約束・節約といった絞るイメージ」をつけておくと覚えやすい
④素因数分解というテクニックを使うと約数が全部で何個あるのか1発で分かり、ケアレスミスが減る
この記事を通じて、最大公約数を求めるのって簡単!と思えるようになってもらえたら嬉しいです。





