パラドックスとは「矛盾・逆説・背反」を意味する言葉です。
正確には「矛盾」よりも意味が広く、見かけ上の真偽と実際の真偽が逆転している説を指します。
● 「一見すると正しそうだけど、実際には正しくない説」
● 「一見すると間違っていそうなのに、実際には正しい説」
今回は、有名なものから少しマイナーなものまで全11個のパラドックスを紹介していきます。
photo credit:brett jordan
①矛と盾
矛盾の語源にもなっている『矛と盾』。
信賞必罰(手柄のあった者には必ず賞を与え、あやまちを犯した者は必ず罰すること)や形名参同（申告と実績を比べて、実績が申告未満だったときはもちろん、申告を大きく超えた実績を挙げたときも罰すること）で有名な『韓非子』に出てくる一説です。
昔、あるところに矛と盾を売る男がいました。
男は矛をこう褒めました。
「この矛はどんな盾も突き通す矛だ」。
また、盾をこう褒めました。
「この盾はどんな矛も防ぐ盾だ」。
そこで疑問に思った客がこう尋ねます。「その矛でその盾を突いたらどうなるのか？」
男は、その質問に答えることができませんでした。
● 矛で盾を突き通せたら→「どんな矛も防ぐ盾」がウソになる
● 盾が矛を防ぎぎったら→「どんな盾も突き通す矛」がウソになる
皆さんは、もし本当に「どんな盾も突き通す矛」と「どんな矛も防ぐ盾」が存在したとしたら、どんな結果になると思いますか？
『突き通せてもいて、防げてもいる』という摩訶不思議な現象が起きるのでしょうか。
②シュレディンガーの猫
「突き通せてもいて防げてもいるなんて現象があるわけないだろう」という方にオススメのパラドックスが、『シュレディンガーの猫』です。
量子力学のミクロな世界では「原子が崩壊していると同時に崩壊していない」という摩訶不思議な現象が起きることが分かっています。
この事実に対し、「これを自分たちがいるマクロな世界に拡張すると『箱の中の猫が死んでいると同時に生きている』という矛盾した現象が起きるのではないか？」と批判するために出てきたたとえ話。
それがシュレディンガーの猫です。
シュレディンガーの猫は元々この矛盾した現象を批判するために出てきた話なのですが、現代では「シュレディンガーの猫は存在しうる」可能性も示唆されており、最近では量子力学の不思議さを伝えるための話として引用されるようになっています。
③アキレスと亀
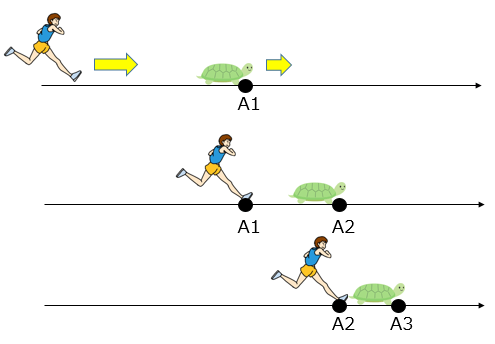
「アキレスがどれだけ速く走ったとしても、前を行くノロマな亀に追いつく事はできない」
有名なパラドックスの1つ『アキレスと亀』です。
まず、アキレスの前方を亀が歩いており、アキレスが走って亀を追いかけたとします。
アキレスが亀に追いつくためには、まず亀がいた地点A1に到達しなければなりません。
亀がいた地点A1にアキレスが到達すると、亀はそれよりも少し進んだ地点A2まで移動しています。
さらに亀がいた地点A2にアキレスが到達しても、亀は再びそれよりも少し進んだ地点A3まで移動しています。
そこでまた亀がいた地点A3にアキレスが到達しても、亀は再び…
と、この話は無限回繰り返せるので、いつまで経ってもアキレスは亀に追いつけません。
普通に考えると「アキレスはすぐに亀に追いつく」はずなのに、この論理通りに考えると確かに「いつまで経っても追いつけない」ように感じてしまいます。
しかし、結論が明らかに間違っている以上、この論理はどこかが間違っているはずなのです。
皆さんは、この論理のどこが間違っているか分かりますか？
④抜き打ちテストのパラドックス
ある週の月曜日の朝、先生はこう言いました。「今週、抜き打ちテストをするぞ」
それを聞いた生徒たちは、こう考えました。
もし、木曜日までにテストが行われなければ、金曜日にテストがあると分かってしまうので金曜日に『抜き打ちテスト』はできない。
金曜日に『抜き打ちテスト』ができないということは、水曜日までにテストが行われなければ木曜日にテストがあると分かってしまうので木曜日も『抜き打ちテスト』はできない。
木曜日も『抜き打ちテスト』ができないということは、火曜日までにテストが行われなければ水曜日にテストがあると分かってしまうので水曜日も『抜き打ちテスト』はできない。
水曜日も『抜き打ちテスト』ができないということは、月曜日までにテストが行われなければ火曜日にテストがあると分かってしまうので火曜日も『抜き打ちテスト』はできない。
ということは月曜日にテストがあると分かってしまうので月曜日も『抜き打ちテスト』はできない。
「つまり、抜き打ちテストは出来ないんだ！」と気づいた生徒たちは、テスト勉強をせずに金曜日までを過ごしました。
すると、なんと金曜日に抜き打ちテストが実施されたのです。
「おかしい！」と怒り出す生徒たちを前に、先生はこう言います。
「でも、今日テストがあるとは予想できなかっただろ？」
⑤ブライスのパラドックス
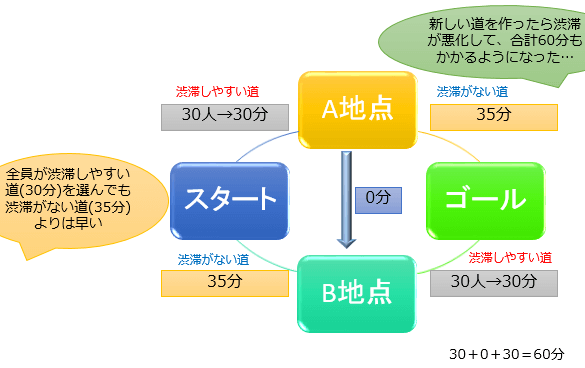
道路が増えた場合、普通に考えると「道が増えたことで移動時間が短縮され、目的地に早く着けるようになる」と思うはずです。
しかし、交通工学の世界では「道が増えたせいでかえって渋滞が悪化して、目的地につくまでの移動時間が長くなってしまう」ケースもあることが分かっています。
それが、『ブライスのパラドックス』です。
都市部などで「ここに道があれば便利なのに…」と思う事があったら、それはもしかしたら『ブライスのパラドックス』のことを考えて「渋滞を悪化させないために、あえて道を作っていない」のかもしれません。
くわしい計算の流れは、合成の誤謬の記事のなかで解説しています。
⑥男か？女か？のパラドックス
「ある人には2人の子供がいて、少なくとも一人は男の子。さて、もう一人の子供が女の子である確率は？」
口語的に考えると答えは1/2なのに、数学用語的に考えると答えが2/3になる。というのがこの「男か？女か？のパラドックス」です。
モンティ・ホール問題と勘違いされやすい話ですが、「問題文に欠陥があって、2通りの解釈ができてしまい、答えが1つに定まらない」のがこのパラドックスの特徴です。
数学の問題としては問題文に欠陥があるのに、それに気がつきにくいのが問題なのです。
もしこの文が「子供が2人いる人に、あなたには息子がいるか？と聞いたらいると答えた。さて、もう一人の子供が女の子である確率は？」という意味なら、答えは2/3となります。
一方この文が「子供が2人がいる人に、あなたの子供の写真を見せてほしいと尋ねたら、息子の写真を見せてもらえた。さて、もう一人の子供が女の子である確率は？」という意味なら、答えは1/2と推定できます。
この話はベイズ推定と呼ばれ、投資やマーケティングの世界でも使われている理論です。
詳しくは、こちらの記事でわかりやすく図解しています。
⑦シンプソンのパラドックス
統計学を知らない人が統計データを読むと、データの意味を読み違えてしまうことが少なくありません。
その原因の1つに、シンプソンのパラドックスがあります。
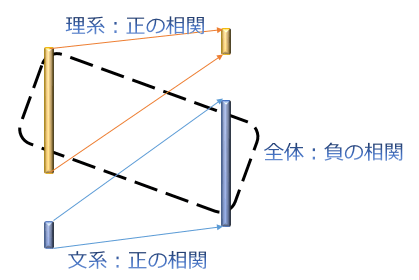
これは、アメリカの統計学者E.H.シンプソンが提示した「集団を2つに分けた場合にある仮説が成り立っても、集団全体では正反対の仮説が成り立つことがある」というパラドックスです。
統計学では相関関係の話で引用されることが多いのですが、相関関係の話は少し難しくなってしまうので、今回はシンプルな話にしてみましょう。
A高校の理系クラスの平均点は、B高校の理系クラスの平均点よりも5点低い
また、A高校の文系クラスの平均点は、B高校の文系クラスの平均点よりも5点低い
しかし、理系と文系を足したA高校全体の平均点は、B高校全体の平均点よりも4点高い
こんな事はあり得るのか？
A高校理系平均 ＜ B高校理系平均
A高校文系平均 ＜ B高校文系平均
A高校全体（理系＋文系）平均 ＞ B高校全体（理系＋文系）平均
答えは「あり得る」です。これがシンプソンのパラドックスの意味するところ。
一見すると「A高校の理系クラスの平均点も文系クラスの平均点もB高校のそれより低いのなら、全体で見ても絶対にA高校の方が平均点は低いはず！」と思ってしまいますが、実はそうでもありません。
下の図を見てください。
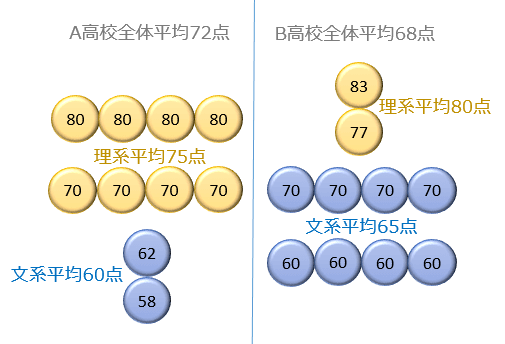
この図は、A高校とB高校の生徒を10人と仮定し、その点数分布を理系・文系で色分けしたものです。
A高校の理系平均は75点で、B高校の理系平均80点よりも5点低い。
また、A高校の文系平均は60点で、B高校の文系平均65点よりも5点低い。
しかし、A高校全体の平均は72点で、B高校全体の平均68点よりも4点高いのが分かります。
このように、分割するサンプルサイズ（今回の場合は理系・文系の生徒数）に大きな差がある場合、シンプソンのパラドックスのせいで「理系だけの評価＋文系だけの評価」と「全体の評価」が正反対になるケースもあることを覚えておきましょう。
⑧誕生日のパラドックス
生まれが「うるう年」ではない、ある学年の話。
そのクラスには23人の生徒がいます。ある日、クラス全員の誕生日を聞いたところ、BさんとC君の誕生日が同じだと分かりました。
「BさんとC君って同じ誕生日なの！？同じクラスで1/365の確率を引き当てるなんて、すごい運命だ！」と皆おおはしゃぎ。
しかし、先生にこの話をすると「よくあることだよ」と冷めた態度でした。
Ｑ：先生の言う通り、これは本当によくあることなのでしょうか？
Ａ：約50.7％の確率で起きること。珍しいことではない。
「実際に確率を計算してみると、直感から大きく外れた値になる」というパラドックスです。
これは、誕生日のパラドックスと呼ばれています。
同じクラスの中には、意外と同じ誕生日のペアが1組はいるものなんですね。
⑨サンクトペテルブルクのパラドックス
偏りのないコインを表が出るまで投げ続け、何回裏が出続けたかで賞金が決まるゲームがあったとしましょう。
「1回目に表が出たら1円」「1回目は裏が出て2回目に表が出たら倍の2円」「2回目まで裏が出たあと3回目に初めて表が出たらそのまた倍の4円」「3回目まで裏が出たあと4回目に初めて表が出たらそのまた倍の8円」という風に倍々でもらえる賞金が増えるとします。
あなたは、このゲームの参加費が何円なら挑戦しますか？
普通に考えると「賞金の期待値よりも参加費が低ければ挑戦した方が得」・「大抵1円～4円しかもらえないのだから、高くても5円くらいまでかな」と思うはずです。
しかし、実際に期待値を計算してみると「たとえ1回の参加費が1万円でも参加した方が得」という結果が出てきてしまう、というのが『サンクトペテルブルクのパラドックス』です。
1回あたりの賞金の期待値が無限大なので、お金に余裕があるならたとえ参加費1万円だろうと100万円だろうと参加した方が得という結果になってしまうのです。
これは明らかに直感に反しますよね。
このパラドックスに対する解答としては、「①単純な期待値計算は実際にはあまり役に立たない②効用関数を用いて計算するべきである③無限回試行できるなら確かに参加費が100万円でも得だが、実際には1億回の試行すら不可能であり、現実的に可能な試行回数では99.99%以上の確率で損をする」などが挙げられます。
⑩バナッハ・タルスキーのパラドックス
「球体を三次元空間内で有限個の部分に分割し、それらを平行移動・回転操作のみを使ってうまく組み替えることで、元の球体と同じ半径の球体を2つ作ることができる」
それが、『バナッハ・タルスキーのパラドックス』です。
何を言ってるか分からないという方のために説明すると「数学理論上は、1つの球体をうまく分解→組み換えすると元と同じ大きさの球体を2つ作ることができる。つまり球体をどんどんと複製できてしまう」という理論です。
『数学理論上は』というのがポイントで、現実世界ではもちろんこんな事は不可能です。
このパラドックスの重要なところは「何1つ矛盾なく数学的論理を積み上げていったのに、球体を複製できてしまうという明らかに直感に反した答えが出てきてしまった」ことにあります。
現実では不可能なことに変わりはないので、数学に興味がない方からしたら「だから何なの？」という話ではあるのですが、数学者にとっては大きな問題でした。
「もしかしたら、自分たちが正しいと信じていた理論のどこかが間違っているのかもしれない」と思わせるような答えだったのですから。
現在では「明らかに直感に反した答えではあるが、数学理論上は可能でも問題ない」と分かり、このパラドックスも解決しています。
⑪2つの封筒問題
ある年の正月、2人の兄弟のもとに叔父さんがやってきて、机の上に2つの封筒を置きながらこう言いました。
「この2つの封筒のうち、1つにはもう片方の2倍の金額が入っている。お年玉としてそれぞれ1つずつ好きな方を選びなさい」
兄弟は適当に選んで封筒のなかを見たところ、お兄ちゃんの封筒には1万円・弟の封筒には2万円が入っていました。
このとき、兄弟は相手の封筒にいくら入っているのかお互いに知りません。
そこで叔父さんはこう言います。
「1回だけ2人の封筒を交換してみないか？2人とも自分が交換した方が得かよく考えてみて」
まず、お兄ちゃんはこう考えます。「自分が安い方の封筒を選ぶ確率は50%。つまり弟の封筒の方が高い確率は50%で、その場合は2万円入っている。逆に弟の封筒の方が安い確率は50%で、その場合は5千円入っている。つまり期待値は1万2500円で、1万円より高いから交換した方が得だ！」
次に、弟もこう考えます。「自分が安い方の封筒を選ぶ確率は50%。つまりお兄ちゃんの封筒の方が高い確率は50%で、その場合は4万円入っている。逆にお兄ちゃんの封筒の方が安い確率は50%で、その場合は1万円入っている。つまり期待値は2万5000円で、2万円より高いから交換した方が得だ！」
実際に交換したら弟が損をするのですが、期待値上は2人とも交換した方が得という変な結果が出てしまいました。
これが『2つの封筒問題』です。
種明かしすると、実は「安い方の封筒を選ぶ確率」と「封筒を開けたら中身が2万円だった場合に、それが安い方の封筒である確率」は、全く違うものなんです。
統計学では前者を事前確率・後者を事後確率と言い、その計算式は明確に異なります。
もし封筒に入っているのが(4万円と2万円)であるパターンと(2万円と1万円)であるパターンの確率が等しければ「たまたま」どちらも50%になるというだけで、両者は実際には全く異なる概念なのです。
＞＞関連記事：ベイズの定理とは何か。条件付き確率からわかる判別の知恵
この問題は「2種類の確率を混同させる」ことで、パラドックスになっています。
ちなみに、「結局、弟は期待値的には交換するべきなのか？」という質問に対しては、「叔父さんが封筒に4万円と2万円を入れている確率」が「封筒に2万円と1万円を入れている確率」の0.5倍より高いと考えられるなら、交換するべきが答えとなります。
では、その確率が全く見当もつかないときはどうするか？…直感で選ぶしかないですね。
