数あるパラドックスの中でも特に有名な話の1つ「アキレスと亀」。
間違っているのは明らかに分かるのに、どこの論理が間違っているのかを説明するのが意外と難しく、よく話題にあがるパラドックスの1つとなっています。
今回は、この「アキレスと亀」の説明とその論破法・そこから派生したお話を取り上げていこうと思います。
アキレスと亀。ゼノンのパラドックスとは?
アキレスと亀とはゼノンのパラドックスの1つ。
「アキレスがどれだけ速く走ったとしても、前を行くノロマな亀に追いつく事はできない」という話のことを指します。
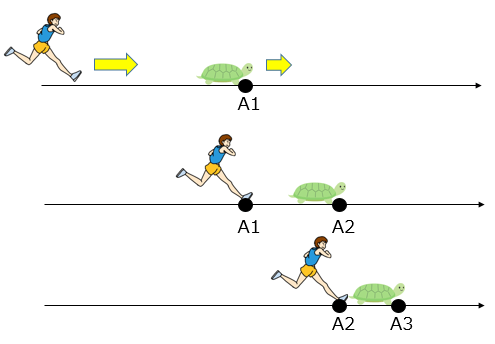
まず、アキレスの前方を亀が歩いており、アキレスが走って亀を追いかけたとします。
アキレスが亀に追いつくためには、まず亀がいた地点A1に到達しなければなりません。
亀がいた地点A1にアキレスが到達したとき、亀はそれよりも少し進んだ地点A2まで移動しています。
さらに亀がいた地点A2にアキレスが到達しても、亀は再びそれよりも少し進んだ地点A3まで移動しています。
そこでまた亀がいた地点A3にアキレスが到達しても、亀は再びそれよりも(中略)
(中略)・・・そこでまた亀がいた地点A100にアキレスが到達しても、亀は再び(以下略)
と、この話は無限に繰り返せるので、いつまで経ってもアキレスは亀に追いつけないというお話です。
普通に考えれば「アキレスはすぐに亀に追いつく」に決まっているのに、この話を初めて聞いたときは「あれ?本当に追いつけないぞ?」と納得しそうになりますよね。
論破されるためのお話
このパラドックスは、古代ギリシアの哲学者ゼノンによって唱えられました。
しかし、別にゼノンはこのパラドックスで「アキレスは亀に追いつけない」というトンデモ理論を主張したかったわけではありません。
 By: Antonio Campoy
By: Antonio Campoy
当時、古代ギリシアにはピタゴラス学派と呼ばれる人々がおり、ゼノンは「あの派の主張は誤りである」と批判するためにこのパラドックスを唱えたとされています。
つまり「あの人たちの主張が正しいとするとこんな変なコトが起きることになるけど、実際はそんなことないよね?おかしくない?」と皆に問いかけたということ。
「確かに、この話は間違っている!つまりピタゴラス学派の主張は誤りなんだ!」
と論破されるためのお話なんです。
しかし、哲学的な話を知らない現代人でも、このパラドックスはある思い込みを捨てないと、一瞬納得しかけてしまいますよね。
『一般人でも納得しかけるほどパッと見の理屈が通っているが、ある思い込みを捨てることさえできればカンタンに論破できる』
それこそがアキレスと亀の話の面白いところであり、長く語り継がれている理由なのでしょう。
 By: foshie
By: foshie
1.999999と無限
アキレスと亀の話で間違っているのは「この話は無限に繰り返せるので、いつまで経ってもアキレスは亀に追いつけない」という部分にあります。
無意識のうちに「無限に繰り返せる(話が無限に続く)」を「いつまで経っても追いつかない(無限の時間かけても追いつかない)」と混同しているのが問題なんです。
アキレスと亀の話は、アキレスが秒速1m・亀が秒速0.1mと考えると分かりやすいです。
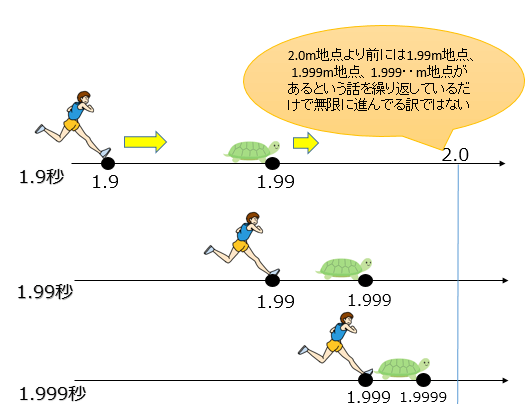
スタートから1.9秒後、アキレスは1.9m地点・亀は1.99m地点(A1)にいたとします。
スタートから1.99秒後、アキレスは1.99m地点(A1)・亀は1.999m地点(A2)にいます。
スタートから1.999秒後、アキレスは1.999m地点(A2)・亀は1.9999m地点(A3)にいます。
この話は1.999999…秒後と無限に繰り返すことができますが、だからといって「アキレスは亀に追いつくのに無限秒かかるか?」と言えば明らかに間違っていることが分かるはずです。
つまり「1.99よりも大きな1.999よりも大きな1.9999…と話は無限回続く」という回数の無限と「いつまで経っても」という時間や距離の無限を混同しているのが問題だったんです。
これは、「無限」という身近にはないはずの概念が、有限の世界にいきなり現れるとビックリしてしまうのが混同する原因と考えられます。
この辺りは「整数による分数では表せない」せいで小数点以下の数が無限に続く円周率を不思議に感じてしまうのに似ているなと思います。

論破例)この話は誤っている。なぜなら「話を無限回くり返せるならば、いつまで経っても追いつかない」という主張は誤りだからだ。「回数の無限」と「時間や距離の無限」は違う。仮に2秒後に追いつくとしても1.9秒後、1.99秒後、1.999秒後、1.9999秒後と刻んでいけば話を無限回くり返すことができる。この話は「アキレスは、亀に追いつく直前までは亀に追いつけない」という当たり前のことを、無限回の試行に言い換えているに過ぎない。
無限個の足し算の答えが有限になる
アキレスと亀の話の面白いポイントは、もう1つあります。
それは「無限個の足し算の答えが有限になる」ということです。
普通は「1+1+1+1…」と無限個の足し算をすると答えも無限になりますが、「1+0.9+0.09+0.009+…」では無限個の足し算であっても答えは2に近づいていくだけなんです。
「無限の先に有限がある」というのは、面白い話ですよね。
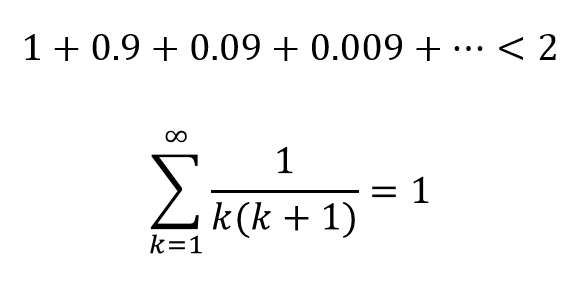
これは、数学上の表現では「無限級数が有限の値に収束する」と呼ばれています。
この「無限級数が有限の値に収束する」話は、高校数学以外でも物理学や統計学など幅広い領域で出てくる概念です。
まとめ
①アキレスと亀とは、「アキレスがどれだけ速く走ったとしても、前を行くノロマな亀に追いつく事はできない」という話のこと。
②ゼノンは「アキレスは亀に追いつけない」というトンデモ理論を唱えたのではなく、ピタゴラス学派を批判するためにこのパラドックスを唱えた。
③一般人でも一瞬納得しかけるが、ある思い込みを捨てることさえ出来ればカンタンに論破できる。それがアキレスと亀の話の面白いところ。
④この話で間違っているのは「無限に繰り返せるので、いつまで経ってもアキレスは亀に追いつけない」という部分。「回数の無限」と「時間や距離の無限」を混同しているのが誤りの原因。
⑤「無限個の足し算の答えが有限になることもある」というのも面白いポイント。これは高校数学はもちろん、物理・統計学でも使われている話。
ぼく自身、アキレスと亀の話は小学生のときに塾の先生から教えていただいたのですが、あの時の「絶対に間違っているのは分かるのにキレイに説明しきれない」歯がゆさは今でも覚えています。
この記事が、算数や数学・論理的思考の面白さを感じるキッカケになれば嬉しいです。