ベクトルは、向きと大きさだけをもった量です。
ベクトルには「位置情報」がありません。
これは「平行移動について考えやすくなる」という利点でもある一方で、「特定の性質をもつ点の位置について考えることができない」という欠点でもあります。
そこで、「特定の性質をもつ点の位置を調べたい」ときに使えるのが位置ベクトル(Position Vector)です。
位置ベクトルとは、原点を始点とするベクトルのこと。
始点を固定することにより、内分点・外分点・重心・垂心・内心といった特殊な点の位置を一般化して考えたいときに便利な存在となっています。
今回は、そんな位置ベクトルについて解説していきます。
位置ベクトルとは
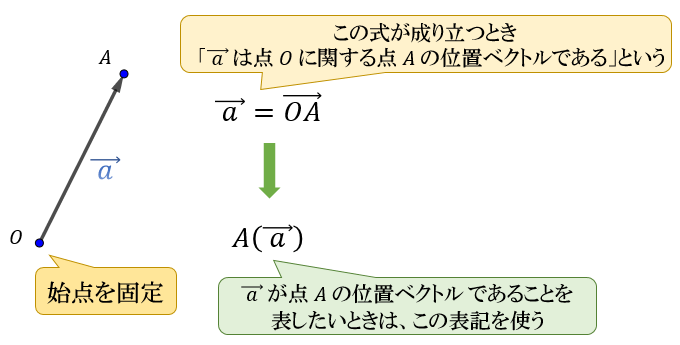
平面上で点 \(O\) を固定して考えると、点 \(A\) の位置は \(\vec{\ a\ }=\vec{OA}\) で表わすことができます。
このとき、「\(\vec{\ a\ }\) は点 \(O\) に関する点 \(A\) の位置ベクトルである」といい、\(A(\vec{\ a\ })\) で表します。
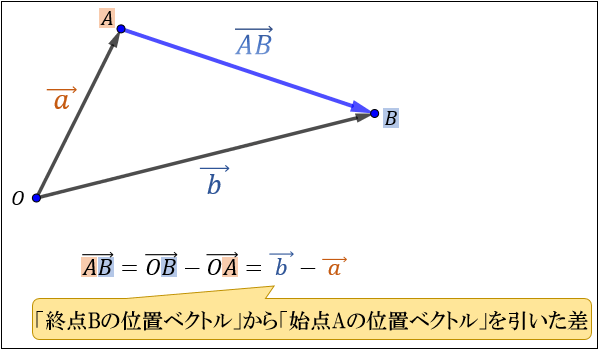
ここで、2点 \(A(\vec{\ a\ })\),\(B(\vec{\ b\ })\) を結ぶベクトルは、\(\vec{AB}=\vec{\ b\ }-\vec{\ a\ }\) となります。
内分点の位置ベクトル
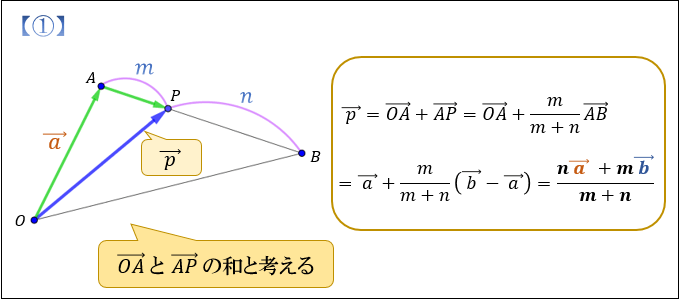
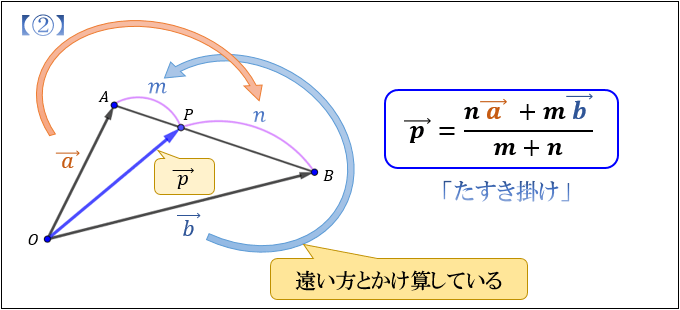
2点 \(A(\vec{\ a\ })\),\(B(\vec{\ b\ })\) を結ぶ線分 \(AB\) を \(m:n\) に内分する点を \(P\) とすると、その位置ベクトルは\(\vec{\ p\ }=\dfrac{n\vec{\ a\ }+m\vec{\ b\ }}{m+n}\) で表すことができます。

【問1】2点 \(A(\vec{\ a\ })\),\(B(\vec{\ b\ })\) に対して、線分 \(AB\) を \(2:3\) に内分する点を \(P\) としたとき、 点 \(P\) の位置ベクトル \(\vec{\ p\ }\) を \(\vec{\ a\ }\),\(\vec{\ b\ }\) を使って表してください。
答え:\(\vec{\ p\ }=\dfrac{3 \vec{\ a\ }+2 \vec{\ b\ }}{5}\)
外分点の位置ベクトル
2点 \(A(\vec{\ a\ })\),\(B(\vec{\ b\ })\) を結ぶ線分 \(AB\) を \(m:n\) に外分する点を \(Q\) とすると、その位置ベクトルは\(\vec{\ q\ }=\dfrac{-n\vec{\ a\ }+m\vec{\ b\ }}{m-n}\) で表すことができます。

\(m:-n\) に内分する点と考えると「内分点の位置ベクトルの公式」からも求められる
【問2】2点 \(A(\vec{\ a\ })\),\(B(\vec{\ b\ })\) に対して、線分 \(AB\) を \(5:2\) に外分する点を \(Q\) としたとき、 点 \(Q\) の位置ベクトル \(\vec{\ q\ }\) を \(\vec{\ a\ }\),\(\vec{\ b\ }\) を使って表してください。
答え:\(\vec{\ q\ }=\dfrac{-2 \vec{\ a\ }+5 \vec{\ b\ }}{3}\)