因数分解の公式まとめ一覧とその活用例

④の公式に $a=y,b=y$ を代入すると①の公式になり、$a=-y,b=-y$ を代入すると②の公式になり、$a=y,b=-y$ を代入すると③の公式になります。

④の活用例

$x^2+7x+12=x^2+(3+4)x+3×4$

$=(x+3)(x+4)$

$x^2-x-6=x^2+(-3+2)x+(-3)×2$

$=(x-3)(x+2)$

$x^2-4x-45=x^2+(-9+5)x+(-9)×5$

$=(x-9)(x+5)$

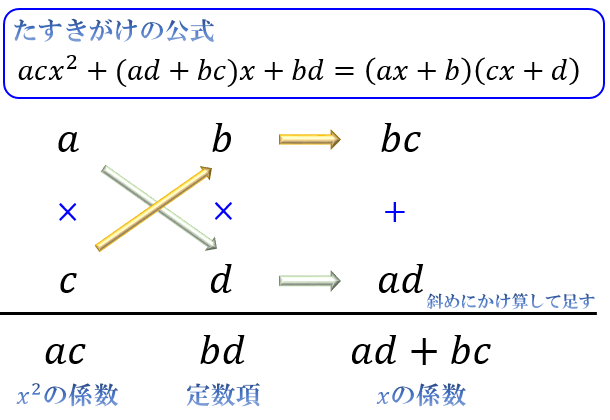
活用例

$3x^2+x-2=(3x-2)(x+1)$

⇒ $ac=3,bd=-2$ を満たす $a,b,c,d$ を組み合わせて $ad+bc=1$ を作る

$4x^2-4x-15=(2x-5)(2x+3)$

⇒ $ac=4,bd=-15$ を満たす $a,b,c,d$ を組み合わせて $ad+bc=-4$ を作る

活用例

$x^3-8=(x-2)(x^2+2x+4)$

⇒⑥の公式に $y=2$ を代入

$x^3-3x^2+3x-1=(x-1)^3$

⇒⑧の公式に $y=1$ を代入

活用例

$x^2+y^2+1+2xy+2x+2y=(x+y+1)^2$

⇒⑨の公式に $a=x,b=y,c=1$ を代入

$x^3+2x^2-5x-6=(x+1)(x-2)(x+3)$

⇒⑪の公式に $a=1,b=-2,c=3$ を代入