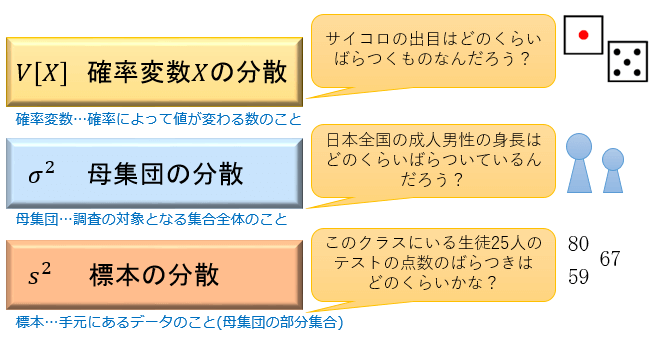
分散とは、データのばらつきの大きさを表す指標です。
分散は「日本全国の成人男性の身長はどのくらいばらついているのか?」を考えたり、「\(n\)個のサイコロの出目の合計は期待値からどのくらい離れた値になるものなのか?」を考えるのに便利な値です。
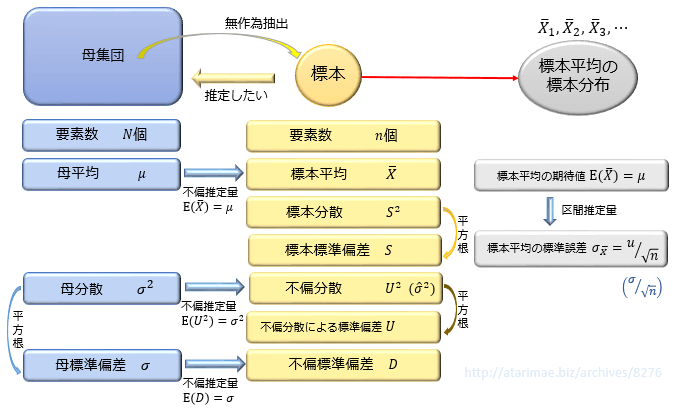
n個のデータの分散の求め方
\(n\)個のデータ \(x_1,x_2,\cdots,x_n\) について、以下の式で表される値 \(s^2\) を分散と言います。
標本分散と呼ばれることも多いです。

\(n\) の代わりに \(n-1\) で割った値は不偏分散と呼ばれ、母集団の分散 \(σ^2\) の推定に用いられます。詳しくは「分散や標準偏差において n-1 で割る公式の理由」の記事を参考にしてください。
さっそく、以下の4人(A,B,C,D)の点数について、数学の点数の分散を求めてみましょう。

step①平均値を求める
分散を求めるには、まず平均値を求める必要があります。
平均値は、データのすべての値を合計してデータの総数 \(n\) (今回は \(4\) )で割ることで求まります。
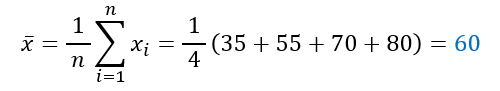
平均値が \(\overline{x}=60\) 点と求まりました。
step②偏差を求めて、2乗する
平均値が求まったら、次は偏差を求めます。
偏差とは、各データの値から平均値を引いた値です。
今回は平均値が \(\overline{x}=60\) なので、各 \(x_i\) から \(60\) を引くと偏差が求まります。
偏差が求まったら、それらをすべて2乗していきましょう。
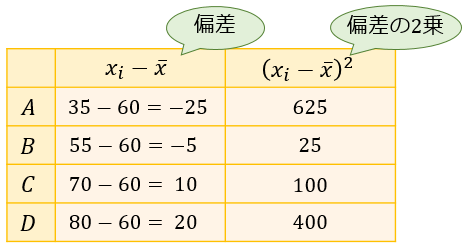
step③偏差の2乗を合計してデータの総数で割る
偏差の2乗が求まったら、それらを合計してデータの総数 \(n\) (今回は \(4\) )で割ると、分散が求まります。
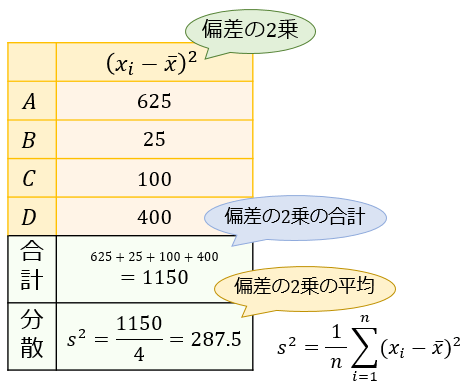
ここから、「4人(A,B,C,D)の数学の点数の分散は \(287.5\) だ」と言うことができます。
分散はデータのばらつきの大きさを表してはいますが、「ばらつきの大きさが \(287.5\) だ」と言われても直感的に分かりにくいですよね。
分散の意味を感覚的に分かりやすくするには、分散の正の平方根である標準偏差を利用します。
これについては「標準偏差とは何か?その求め方や公式の意味・使い方」の記事で詳しく解説しているので参考にしてみてください。
確率変数の分散の求め方
確率変数 \(X\) について、以下の式で表わされる値 \(V[X]\) を「確率変数 \(X\) の分散」と言います。


step①期待値を求める
まずは、確率変数 \(X\) の期待値を求めます。

step②偏差を求めて、2乗する
期待値が求まったら、次は確率変数の取りうる値から期待値(今回は \(μ=340\) )を引いて偏差を求めます。
偏差が求まったら、それらをすべて2乗していきましょう。

step③偏差の2乗の期待値を求める
偏差の2乗が求まったら、「偏差の2乗の期待値」を計算すると、分散が求まります。

ここから、「確率変数 \(X\) の分散は \(60400\) だ」と言うことができます。
覚えておきたい分散の公式
分散について特におさえておくべき公式は以下の5つです。
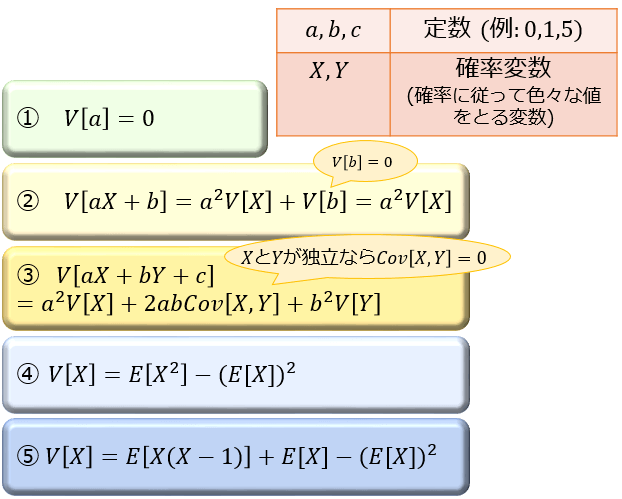
①は「定数は確率によるバラツキが \(0\) 」という意味です。
「\(1\) はずっと \(1\) のままでばらつかない」ですよね。
重要なのが④の公式で、式変形した\(E[X^2]=V[X]+(E[X])^2\) の形でもよく使います。
統計学の試験でも頻出の公式なので、絶対に覚えておきましょう。
⑤の公式は④と比べると使用頻度は少ないですが、ポアソン分布の分散を求めるときなんかに便利ですね。
③の\(Cov[X,Y]\) は確率変数 \(X\) と \(Y\) の共分散です。共分散については「共分散とは?その求め方と解釈。2変数データや2つの確率変数の関係性」の記事で解説しています。