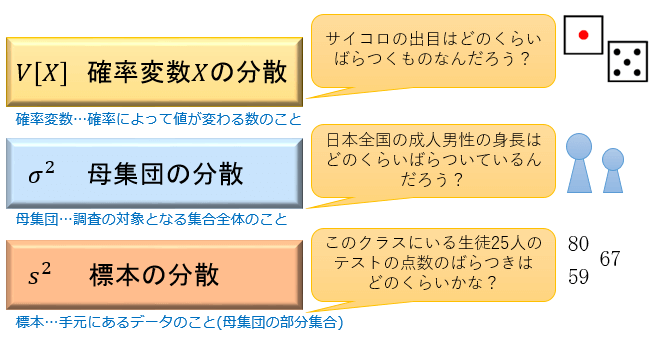
日本全国の20代男性の平均身長を知りたい場合、何百万といる20代男性全員のデータを集めるのは、時間とコストがかかりすぎてしまうので現実的ではありません。
代わりに使われているのが、無作為に選んだ数百人のデータを集めて「その数百人の20代男性の平均身長 \(\overline{X}\)」を「日本全国の20代男性の平均身長 \(μ\) の推定値」として利用する方法です。
ただ、この方法には1つ懸念材料があります。
それは、「たまたま身長の高い人ばかりを調査してしまったら、真の平均から大きく離れた統計結果になってくるのではないか?」ということ。
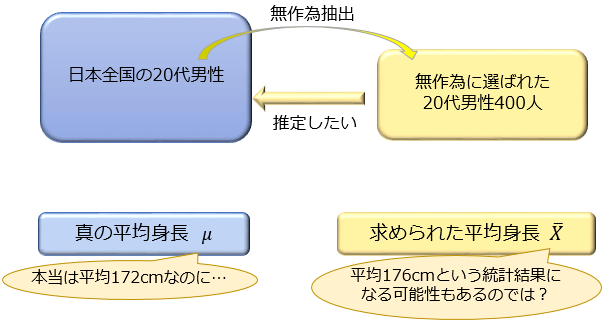
このような不安を抱えたままでは、せっかく得られた統計結果をどのくらい信頼していいか分かりません。
そこで重要になってくるのが、「真の平均からどのくらい誤差のある統計結果になる確率がどのくらいあるのか」を知ることです。
例えば「無作為抽出によって得られる平均身長 \(\overline{X}\) は、\(95\)% の確率で真の平均身長 \(μ\) との誤差 \(0.5\) cm以内に収まる」と分かっていれば「今回、無作為抽出によって得られたデータの平均身長は \(172.1\) cmでした」といった統計結果についてどのくらい信頼していいか検討がついてきますよね。
この「真の平均からどのくらい誤差のある統計結果になる確率がどのくらいあるのか」を近似的に説明する定理。
それが、中心極限定理です。
中心極限定理とは?
中心極限定理とは、ざっくり言ってしまうと
「\(n\) 個の標本平均の確率分布は \(n\) が十分に大きければ平均 \(μ\) 分散 \(\frac{σ^2}{n}\)の正規分布に近似できる」
という定理です。
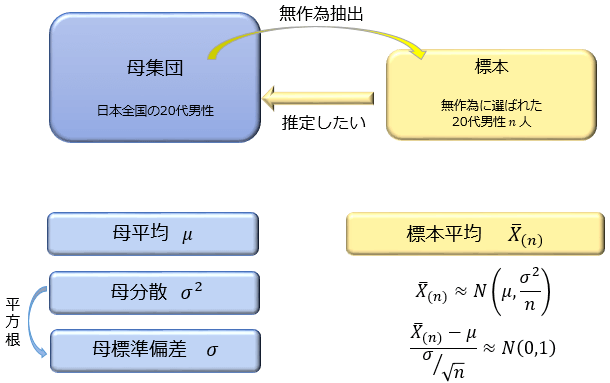
【中心極限定理】
互いに独立な確率変数 \(X_1,X_2,\cdots,X_n\) が母平均 \(μ\) 母分散 \(σ^2\) の同一の確率分布に従うとき、 標本平均 \(\overline{X}_{(n)}=\frac{X_1+X_2+\cdots+X_n}{n}\) にたいして、確率変数 \(Z=\frac{\overline{X}_{(n)}-μ}{σ/\sqrt{n}}\)は \(n \to \infty\) のとき正規分布 \(N(0,1)\) に従う
厳密には \(n \to \infty\) について述べた定理ではあるのですが、早いものなら \(n=100\) 程度、そうでなくても \(n=1000\) 程度あれば大抵のケースで正規分布に近似できてしまうのが中心極限定理の特徴です。

サイコロで分かる中心極限定理
中心極限定理を理解するために、\(n\) 個のサイコロの出目の平均の確率分布を見ていきましょう。
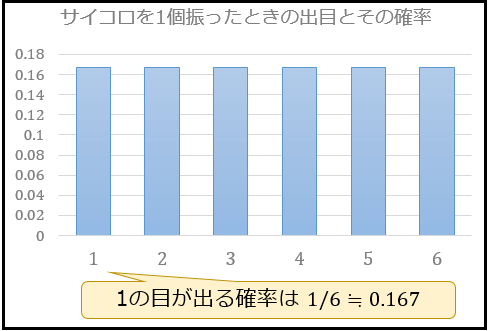
まず、サイコロを1個だけ振った場合、1から6の目が出る確率はそれぞれ \(1/6≒0.167\)。
よって、サイコロを1個振ったときの出目の確率分布は以下のようになります。
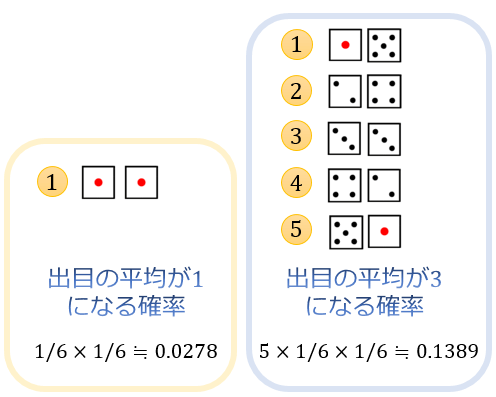
次に、サイコロを2個振ったときに出目の平均が1になる確率は、2個とも1の目が出ればいいことから \(1/6×1/6=1/36≒0.0278\)。
サイコロを2個振ったときに出目の平均が3になる確率は、(1,5)(2,4)(3,3)(4,2)(2,5)の5通りのどれかが出ればいいことから \(5×1/6×1/6=5/36≒0.1389\)。
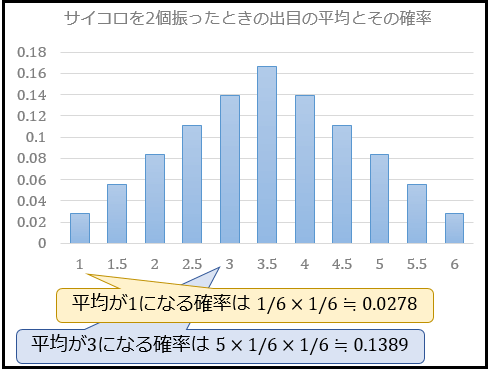
これを全パターンについて計算すると、サイコロを2個振ったときの出目の平均の確率分布は以下のようになります。
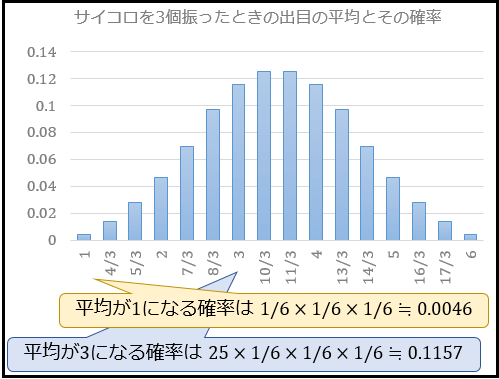
同様に、サイコロを3個振ったときの出目の平均の確率分布。
さらに、サイコロを10個振ったときの出目の平均の確率分布。

サイコロの個数 \(n\) を増やすことで、その出目の標本平均 \(\overline{X}_{(n)}=\frac{X_1+X_2+\cdots+X_n}{n}\) の確率分布が正規分布に近い形になっていくことが分かります。
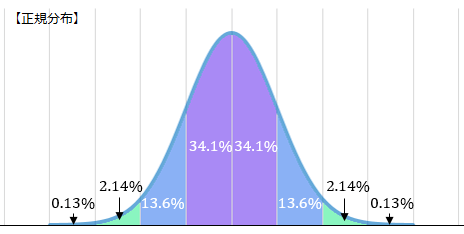
具体的には、\(n=10\) では「平均 \(μ=\frac{7}{2}\)、分散 \(\frac{σ^2}{n}=\frac{35}{12×10}\)の正規分布 \(N(\frac{7}{2},\frac{35}{120})\)」に近い形をしていることが分かります。
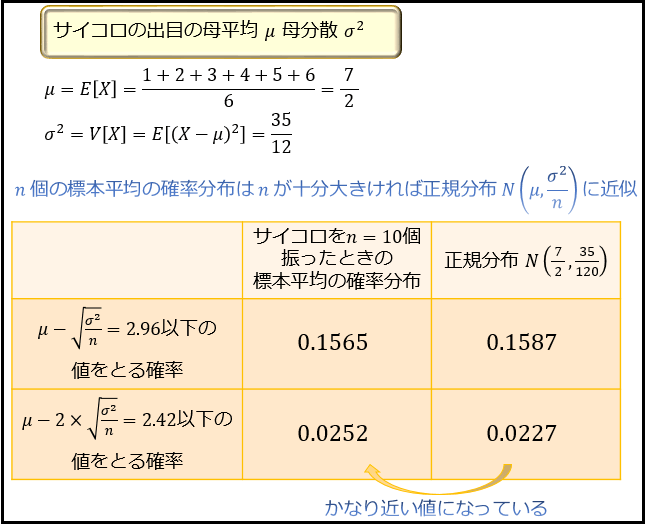
\(n=10\) でここまで近づいているのですから、\(n=100\) や \(n=1000\) ならかなり精度の高い近似になることが分かりますね。
このように、単体ではその確率分布が正規分布とは大きく異なる確率変数であっても、\(n=100\sim1000\) も集めればその標本平均の確率分布は正規分布に近似できるというのが中心極限定理の意味するところです。
ごく一部の特殊な例外を除いて、どんな確率変数であってもその標本平均の確率分布が正規分布になるというのは驚きの事実です。
大数の法則と中心極限定理の関係性
先日紹介した大数の法則は「\(n\) が大きければ大きいほど、標本平均 \(\overline{X}_{(n)}\) は母平均 \(μ\) に近い値をとる確率が高くなっていく」という大雑把な話でしかありませんでした。
それに対して、中心極限定理は「標本平均が母平均に近い値をとる確率が高くなっていくのは分かったけど、じゃあ具体的にどのくらいの速度でどのくらい近い値をとりやすくなっていくのか?」を近似的に説明する定理となっています。
様々な統計結果の信頼性の根拠となる、まさに統計学の「中心」的役割を担う「極限定理」と言えますね。